←　前節(§§５−１)へ

↑百問百答目次へ

問　心拍変動を記述する最も基本的な時系列データはどのようになりますか？

答　正常心拍に由来するR波の起源は洞結節において閾値を超える電位変動が生じたか否かという二者択一の事象に帰着します．従って心拍変動を表す最も基本的な時系列データはR波の観測時刻(厳密にはより観測が困難なP波の観測時刻)に値１を，その他の時刻に値０をもつパルス時系列であると考えられます．

問　従来，２つのR波のうち後行するR波の観測時刻をその観測時刻とし，先行するR波との間隔をその観測値とする(時刻，値)の一連をもって解析対象データとすることがおこなわれています．

答　従来法として知られるこのデータ構成法は心拍変動(RR間隔ゆらぎ)の長時間相関を調べる方法として優れたものです．他方，心拍変動の極短時間相関を調べる場合にはデータの構成方法に由来する“誤差”が混入します．

問　従来法に基づいて構成した心拍変動データを周波数解析して高周波数領域の挙動，換言すれば極短時間相関を議論する場合，何か問題がありますか？

答　周波数解析するためには，その他の多くのデータ解析法でも同様ですが，まず原時系列を等間隔化しなければなりません．通常の時系列であれば，例えば不等間隔で観測されたデータを直線補間して等間隔化する処理は，観測間隔を細かくとって得られるであろう滑らかに変化する観測値の系列を近似形を求めていると考えることも可能です．しかし，心拍変動データでは状況が異なります．すなわち，従来法により構成された心拍変動の時系列は本質的に等間隔化できないデータです．等間隔化処理は不可避の操作ですが，このときに持ち込まれる差異は心拍変動データでは必ず原時系列に内包される情報を歪め，失わせる方向に働きます．そしてその影響はナイキスト周波数に近い高周波数領域において著しいと考えられます．

問　心拍変動の極短時間相関を解析する方法としてそのような方法が考えられますか？

答　時間領域の解析方法としては引き続くN 個のRR間隔の統計的性質を明らかにすることが考えられます．ローレンツプロットは N を２としたときのそのような方法のひとつです．また観測値(RR間隔)とその変化率を位相空間の軌跡として描く方法やいわゆるカオス解析なども考えられます．しかしながらいずれの方法も長いデータを必要とし，従ってそこで得られるのはデータ長にわたってならされた“極短時間相関の平均値”です．

問　心拍変動の極短時間相関の時々刻々の様相を捕らえる解析方法はありますか？

答　TARAWA/WIN(心拍変動データの測定とリアルタイム解析に特化したMemCalc)ではじめて導入されたパルス時系列のエントロピーを求める手法はまさにそのような要求に答える，おそらくは唯一の方法です．そこでは５パルス(R波５つ，RR間隔では４つ)または９パルス(R波９つ，RR間隔では８つ)のみからなるパルス時系列のエントロピーが２秒ごとに求められています．解析対象とするパルスの個数(データ長)とセグメント間隔をさまざまに変えれば希望する相関を直接に捉えることができる方法です．

問　心拍変動のパルス時系列はどのように構成するのですか？

答　例えば250Hzにて心電位が測定されたなら，R波の位置に値１を，その他の位置に値０をもつ時系列として構成します．目的によってはその他の周波数に再サンプリングすることももちろん可能です．

問　パルス時系列を周波数解析するとスペクトルはどのようになりますか？

答　例えば図2120上に示されている平均間隔１のパルス時系列のスペクトルは，同図下のようになります．

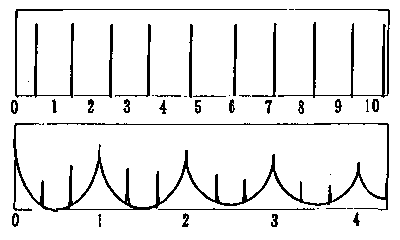
図2120　(上)平均間隔１のパルス時系列と
(下)そのPSD．

スペクトルには平均パルス間隔の逆数，およびその整数倍の位置に顕著なピークが見られます(図2120のスペクトルは縦軸を対数表示した場合のイメージです)．そして顕著なピークの左右にパルス間隔の乱雑さに応じたさまざまな小ピークがほぼ左右対称に並びます．この構造はナイキスト周波数まで繰り返されますが，その形状は周波数とともに不鮮明になります．

問　極短時間相関を問題とするとき，R波のパルス列のスペクトルのどの部分が重要と考えられますか？

答　パルス列の平均間隔を１とするとき，周波数１の顕著なピークを中心とする0.5〜1.5の周波数帯のスペクトルが極短時間相関を強く反映しているようです．この周波数帯のスペクトル構造が高周波数側へナイキスト周波数まで不鮮明になりながらも繰り返されています．また，周波数0.5以下の構造はパルス時系列の長時間相関を反映しているとも考えられます．しかしながら，パルス時系列のスペクトルに見られるこれらの特徴的な挙動に関する透徹した議論が，はたして数理科学の“専門家”によって行われてきたかどうか，はっきりしません．
 

問　 RR間隔変動データ(心拍変動データ)を解析したところ，｢呼吸の影響は評価したか｣との指摘を受けました．

答　複数の因子が心拍変動に影響を及ぼすとき，その影響の仕方が互いに線形の関係であるとき，特定の因子の影響について評価することが可能です．しかし，その影響の仕方が互いに非線形ならば，特定の因子の影響を取り出して評価することは困難です．心拍変動の場合，何れであるか判断する必要があると考えられます．

問　通常の時系列とスペクトルの関係では，周波数 f の付近のスペクトルの挙動は時系列の1/f の時間のオーダの相関を強く反映しています．それから類推するとパルス時系列の高周波数側の挙動はパルス間隔よりも短い時間オーダの相関を反映しているのですか？

答　パルス時系列においては最短のパルス間隔よりも短時間の相関はありません．従ってパルス時系列とそのスペクトルの関係においても，スペクトルの高周波数側の挙動はやはりパルス間隔のゆらぎの反映と考えられます．スペクトルは時系列の自己相関函数のフーリエ変換ですから，フーリエ変換の性質によってスペクトルの各点それぞれは時系列全体の構造を反映しているからです．

問　パルス時系列のエントロピーとはなんですか？

答　パルス時系列を周波数解析してスペクトルを得ます．スペクトル図の縦軸はスペクトル密度で，これは原時系列を構成するさまざまな波のエネルギー(振幅の自乗)が周波数に対してどのように分布しているかを示したものです．されにスペクトル密度の対数ととり，全周波数帯で積分することによりエントロピー密度(エントロピー)が得られます．
 

問　等間隔パルス列のスペクトルはどのようになりますか．それはコンピュータで計算できますか？

答　等間隔パルス列のスペクトルはパルス間隔の逆数の周波数位置，およびその整数倍の位置に高さ無限大・巾無限小の δ 函数が並んだものになります．この δ 函数はディラックの δ 函数(超函数)ですから，コンピュータでは計算できません．

問　しかしTARAWA/WINでは等間隔パルス列のエントロピー値を計算しているのではありませんか？

答　具体的なスペクトルの形状が必要な場合にはパルス列の間隔に微小な乱れを含ませることにより計算できます．具体的には例えば平均パルス間隔の1/200までの精度が求められるとするとき，等間隔パルスの一つをこの最小きざみだけずらすことにより，問題とする精度でもっとも理論値に近いスペクトルを得ることができます．この操作はTARAWA/WINという数値実験装置を用いて測定精度を指定してその範囲でもっとも正確にパルス時系列にエントロピーを測定していることに相当します．

問　TARAWA/WINではエントロピー値を0〜100に規格化して表示しています．それはどのようにして行われますか．またその操作は必ず必要なものですか？

答　注目する周波数帯でエネルギー分布が均一のときの規格化エントロピー値を０，指定精度内でパルス列が等間隔に並んだときの規格化エントロピー値を100として規格化しています．しかしこの規格化は必ずしも必要なものではありません．求めたエントロピー値をそのまま“○○ビット”として表示することも考えられます．また，その場合でも値も心拍数の大小に依存しない値となっています．

問　TARAWA/WINではスペクトルの計算にMEMを用いています．算出したエントロピー値にラグ依存はありませんか？

答　通常の時系列のスペクトルとエントロピーをMemCalcシステムで計算すると，ラグのごく小さな領域(データ点数の数％程度)と極端に大きな領域(データ点数の90％を超える領域)についてはそれらの計算値はラグとともに変動します．他方，相当に広い中間のラグの領域ではスペクトル密度，エントロピー密度ともにほぼ一定値となります．　加えてパルス時系列の場合，ラグを変化させてもラグに相当するデータ長に含まれるパルス数が同じならばスペクトルは変化しません．ラグの長さに含まれるパルス数が変化した場合のエントロピーの挙動ですが，２パルスから３パルス，３パルスから４パルス，４パルスから５パルスと増えるに従ってエントロピー値は変化しますが，その変動は含まれるパルス数の増加とともに急速に小さくなります．実用上，５パルスからなる時系列で３パルス，４パルス，５パルスを含むラグによるエントロピー値の間に差はありません．

↑ページの先頭へ

←　前節(§§５−１)へ

↑百問百答目次へ