|
|
§5 MemCalcとエントロピー
|
|
§§5−1 自己情報量・情報エントロピー
|
|
|
|
スペクトルとエントロピーは対概念としてその重要性が認められてきました.ところがエントロピーについてはこれまで定量的評価に耐えるスペクトルが得られなかったこともあり,実用の場で利用される機会はほとんどありませんでした.
MemCalcはスペクトルとともにエントロピーの値も正確に提示することのできるシステムです.次節におけるMemCalcによるエントロピーの利用にかかわる議論に先立って,本節ではエントロピーとそれにまつわるいくつかの概念についてやや説明的に述べます.この分野の素養のある読者は(本節末の部分エントロピーの定義式以外は)本節を省略してください.
|
|
|
|
|
問 情報とはなんですか? |
1920
|
|
|
|
答 系の状態に関する報せを情報といいます.例えばさいころを振ってどの目が出たかを観測することを考えます.このとき,「1の目が出た」などという報せが情報です.1の目が出たことを(1の目が出るという)事象が生起したといいます.この系は「1の目」〜「6の目」までの6つの事象が等確率で生起する事象系です.
|
|
|
|
|
問 情報量とはなんですか?情報エントロピーとはなんですか?
|
1930
|
|
|
|
答 情報がもたらす系の状態の不確定さの減少分をその情報の(自己)情報量といいます.さいころの例では,最初に観測をおこなう前,系はどの目がでたか全く判らない状態,すなわち不確定度(エントロピー)の高い状態にあります.つぎに観測を行い「1の目が出た」という情報によって系の状態が確定,すなわち不確定度(エントロピー)の低い状態となります.前後のエントロピーの差が自己情報量として取り出された分です.
|
|
|
|
|
問 情報量の多い少ないはどのようにして決まりますか?
|
1940
|
|
|
|
答 より稀な状態が生起したことを報せる情報の情報量をより多く取ります.さいころの例では「奇数の目が出た」という情報と「1の目が出た」という2つの情報を考えます.さいころを振って奇数の目が出る確率は1/2で,他方1の目が出る確率は1/6です.「奇数の目が出た」という前者の情報よりも「1の目が出た」という後者の情報の方が,系がより稀な状態にあることを報せますから,従って後者がより情報量の多い情報となります.情報量
I が確率
p の函数であることを明示するため情報量 I
(p) などの表記が使われます.
|
|
|
|
|
問 ここで扱う情報と日常生活における情報の違いななんですか?
|
1950
|
|
|
|
答 情報科学(Computer Science)における情報は事象の生起確率にのみ依存し,またそのことによってその情報量を一意的に測ることのできるものです.他方,日常生活における情報はそれを受け取る主体にとっての“価値”が常に問題とされます.そこでは同じ生起確率をもつ情報でも,「この宝くじは1等の当たりくじである」という情報とその他の情報では(通常は)前者の方が価値があるとされます.
|
|
|
|
|
問 どのようにして情報の量を定量的に表しますか?また,情報量の加法性とはなんですか?
|
1960
|
|
|
|
答 系が同じ状態にあることを報せる複数の情報があるとき,それらが等しい情報量を伝えることを要請することにより,合理的に情報量を定義することができます.例えばさいころの1の目が出たことを直接に報せる情報の情報量
I0 ,奇数の目が出たことを報せる情報量I1,そして奇数の目が出たことを知ったうえでそれが1の目であることを報せる情報量
I2 の三者の間に次の関係(情報量の加法性)を要請します.
情報量は事象の生起確率のみの函数ですから,上式はそれぞれの生起確率
p0 = 1/6,p1 =
1/2,p2
= 1/3を用いて,
|
I
(1/6) = I (1/2) +
I (1/3) |
となります.
を満足するすべての p0,p1,p2
ついて情報量の加法性,
| I (p0 =
p1 × p2)
= I (p1)
+ I (p2) |
を満たす初等函数は対数函数です.従って確率
p の事情が生起したことを報せる情報の量(情報量,自己情報量)を次式で定義します.
ここに負号は情報量を正の値にとるためです.また,自己情報量とは具体的なその報せ自身が担う情報量という意味です.
|
|
|
|
|
問 情報量の単位はなんですか?
|
1970
|
|
|
|
答 確率 p
で生起する事象が実際に生じたことを報せる情報の自己情報量を与える式,
において対数の底を2にとれば情報量の単位はビット,10にとればデジット,自然対数の底
e (= 2.71828...)にとればナットになります.1ビットの情報量とは二者択一の事象が生じたことを報せる情報のもつ情報量,1デジットとは10者択一の,そして1ナットとは
e 者択一の事象が生じたことを報せる情報のもつ情報量です.また,それぞれの単位は次式の関係により換算されます.
| log x y
= log z y / log z
x |
したがって,1デジット=3.22ビット,1ナット=1.443ビットなどとなります.なお,系のエントロピーの差として取り出されたものが情報量ですから,エントロピーの単位も情報量の単位と同じになります.
|
|
|
|
|
問 自己情報量とはなんですか.例えばさいころで1の目が出たことを報せる情報の自己情報量はどれほどですか?
|
1980
|
|
|
| 答 さいころの1の目で出る確率は1/6です.従って自己情報量の定義式,
に生起確率 p =1/6を代入して.
| I (1/6)
= -log(1/6) = 2.585(ビット) |
(2) |
となります.6者択一の事象が生じたのですから,その報せの情報量は4者択一の場合の2ビットより多く,8者択一の場合の3ビットよりは少ない値となります.
以上の議論は系の状態に関する具体的な報せを得た場合の,その報せのもたらす情報量(自己情報量)についてのものです.他方,系がさまざまな確率で時々刻々異なる状態にあることが判っているとき,多数回の観測を行った場合に得られるであろう1情報あたりの情報量をあらかじめ見積もることができます.
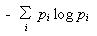 |
(3) |
ここに添え字 i
はすべての場合についてとります.
|
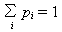
|
(4) |
(3)式は自己情報量の期待値となっており,平均情報量と呼ばれます.
|
|
|
|
|
問 例えばさいころで1の目が出たという報せを受け取る前後で,系のエントロピーはどのように変化しますか?
|
1990
|
|
|
答 報せを受ける前の系のエントロピーをE0,報せを受けた後のそれをE1,この報せの自己情報量をI
とするとき,
自己情報量は正の値をもちますから,報せを受けたあとでは系のエントロピーは減少していることになります.このとき,問題とされるのは常に取り出される(自己)情報量,すなわち系のエントロピーの減少分であって,エントロピーの絶対値ではないことは重要です.このことは逆に系のエントロピーの基準を任意にとれることを意味します.上の例では,
ととれば,
となります.情報量とエントロピーとは負号を除いて等しいことから,しばしば情報量の意味でエントロピーという語が用いられます.
|
|
|
|
|
問 ある事象の生起確率が0〜1まで分布するとき,その事象の発生を報せる情報の量,自己情報量はどのようになりますか?
|
2000
|
|
|
|
答 ある事象 a
が生起する確率をpとするとき,自己情報量
I (p)は次のようになります. |
|
|
|
|
表2000 確率pに対する
自己情報量 I (p). |
|
| p |
I (ビット) |
| 0.00 |
∞ |
| 0.01 |
6.644 |
| 0.05 |
4.322 |
| 0.10 |
3.322 |
| 0.20 |
2.322 |
| 0.30 |
1.737 |
| 0.40 |
1.322 |
| 0.50 |
1.000 |
| 0.60 |
0.737 |
| 0.70 |
0.515 |
| 0.80 |
0.322 |
| 0.90 |
0.152 |
| 1.00 |
0.000 |
|
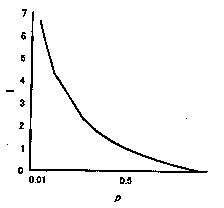
図2000 確率p
に対する自己情報量I (p).
|
|
|
|
問 例えば大きなケーキを
N 人に分配することを考えます.どのように分配されたかを報せる情報の量を合理的に決めたいと思い,次のように考えました.N
= 2のとき,AさんとBさんを区別しないことにすれば,
| 1.一方にp =
p1(0〜1)の分配があった, |
|
2.同時に他方にp = p2
= 1 - p1の分配があった, |
|
3.従って確率p1で生起する確率事象とp2で生起する確率事象がともに起こったと考え,それらの自己情報量の単純和を目安とした,
|
| -
logp1 - logp2 |
ところがこのようにすると分配する人数
N によってその情報量が大きく変化してしまいます.この点を解決し,かつ均等に分配されたときの情報量がN
によらず一定値(例えば0)となるような方法はありませんか? |
2010
|
|
|
答 この情報量
J を次式により定義すれば2つの問題がともに解決できます.
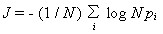 |
(1) |
とくに均等に配分されたとき(pi
= 1 / N )に N pi
は1となり,その対数は0,従ってN
の値にかかわらず均等分配の場合には情報量 J が常に0となることが保証されます.N
が2の場合に(1)式で定義された情報量 J
が一方へ分配された割合
p (0〜1)に伴ってどのように変化するかを図2010に示します.
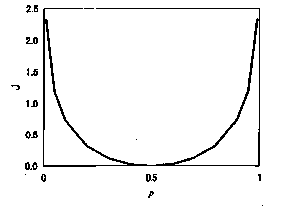
図2010 確率pに対する式(1)で定義された情報量J.
図より,情報量 J
は0,または正の値をもち,その大きさは均等配分からのずれの程度を表していることがわかります.
|
|
|
|
|
問 ケーキをN
人に分配する問題で,N
→∞の極限では情報量 J はどのようになりますか?
|
2020
|
|
|
答 x
= 0〜1で値をもつ確率密度函数 p
(x )を導入することにより,情報量
J は次式となります.
積分は0〜1の区間で行われます.ここに
p (x ) は0,または正の値をもち,0〜1で積分すると1になる函数です.p
(x
)の平均値は1であること,また1を超える値を持ち得ることに注意してください(微小区間での
p (x
)
の積分値,すなわち確率は0以上1以下の値となります).
|
|
|
|
| 問 1Hzあたりの情報量とはなんですか? |
2030
|
|
|
答 スペクトルとそのエントロピーは対概念であると考えられてきました.しかしながら今日まで,スペクトルのエントロピーを定量的に求める事はほとんど行われてきませんでした.これはその元になるスペクトル自体を精度よく求める事ができなかったからです.このような状況はMemCalcシステムの登場により変化しました.定量的評価に耐え得るスペクトルを容易に得る事ができるようになったのです.
エントロピーはその定義から全周波数帯で定義されます.MemCalcではこの定義と情報エントロピーの定義から周波数帯ごとの部分エントロピーを定義し,それを計算・表示しています.ご質問の1Hzごとの情報量は以下の展開の(17)式で与えられる量です.

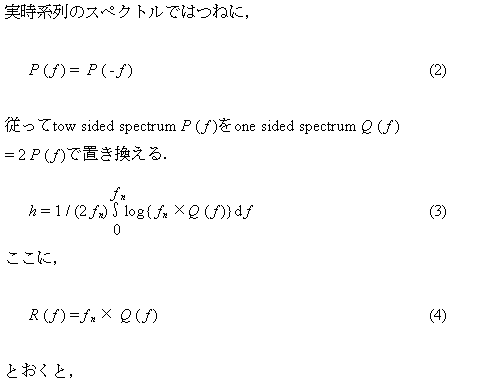







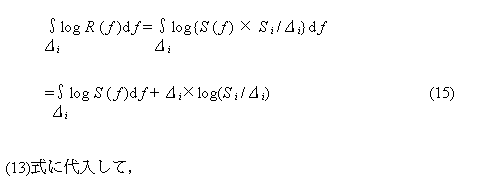
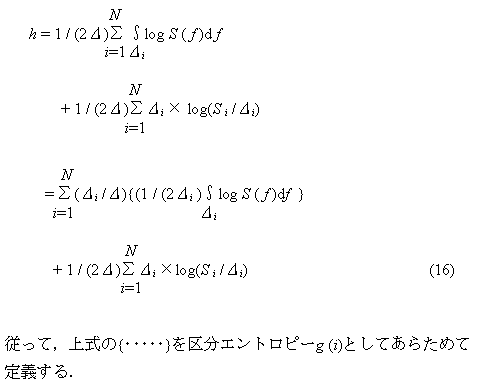

|
|
|
|
|
問 エントロピーを求めるとき,それはラグに依存しませんか? |
2040
|
|
|
|
答 エントロピーはラグを増大させると順次減少します.この減少は緩やかであり,横軸にラグを,縦軸にエントロピーをとってプロットすると,広いプラトー領域が存在します.この挙動のため,特にラグ値を指定しなくても“時系列の(スペクトルの)エントロピーの値”を考察する事が可能です.もちろんラグ値を指定してエントロピーを示せば一切問題は生じません. |
|