↑百問百答目次へ

→　その２(/２)へ

答　時系列(あるいは時系列データ)とは，観測値が時間の経過とともに次々に得られた場合，これらの観測値を時間の順序に従って並べた系列として定義されます．ここで“時間の順序に従って並べた系列”ということに含意される内容を正しく理解することが重要です．

問 “時間の順序に従って並べた系列”ということに含意される内容を正しく理解することがなぜ重要なのでしょうか？

答　時系列における任意時刻の値は，それ以前の時刻の値に何等かの影響を受けており，また，未来の値は過去から現在までの推移に何等かの影響を受けています．従って，その時刻の値は厳密にはその直前までの値に規定されており，時系列の並びを入れ換えたり，値を勝手に変えたりすることは，その時系列に内在する相互連関構造(あるいは単に相関構造)を断ち切ることになり許されません．
　例えば，図0020に示す例は，時系列データの前半と後半を入れ換えた場合，元の時系列の周期構造が全く違ったものになることを示しています．この例は24時間にわたり測定された血圧データです．さまざまな時刻から測定が開始された多数のデータを午前０時を起点に整理しようとして，かつてこうした誤った処理が行われていました．

図0020　時系列データの並びを入れ換えた場合の周期構造(左中)と原時系列データの周期構造(右中)の比較．

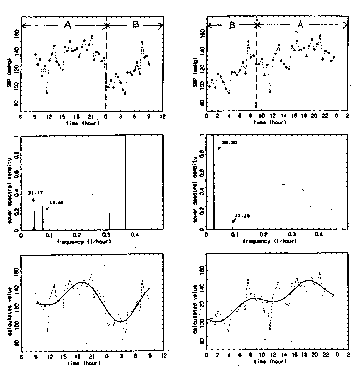
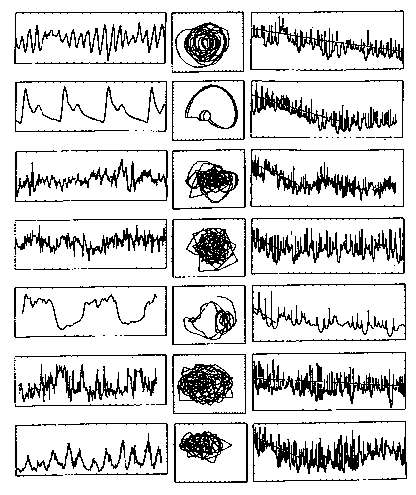
答　図0030に，例として，生物・医学分野の時系列(生体時系列)を示します．上から順に，脳波，血圧脈圧波，心拍数，血圧，体温，行動量，水痘症発生数の時系列デ−タ(左)，相関トラジェクトリー(中)そしてパワースペクトル(右)であり，表0030にデ−タ値の単位，サンプリング時間間隔，デ−タ長をまとめてあります．このように，デ−タの種類によって，時系列の変動パターンは大きく変わります．また，サンプリング時間間隔，デ−タ長の違いによっても，時系列の変動パタ−ンはお互いに全く異なりますし，同じ種類のデ−タであっても，時間領域によって変動パタ−ンは異なります．これは時系列一般に見られる特質です．

図0030　生体時系列の例.上から順に，脳波，血圧脈圧波，心拍数，血圧，体温，行動量，水痘症発生数の時系列データ(左)，相空間トラジェクトリー(中)，パワースペクトル(右)．

　

表0030 図0030に示した生体時系列データの測定条件．

問　データの種類やデータ長，時間領域によって時系列が違うのは理解できますが，同じデータでもサンプリング間隔で変動パターンが違うとはどういうことですか？

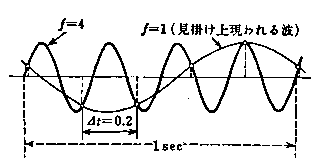
答　現象を記録する時間点をサンプリング(標本)時間と呼びますが，例えば図0040に示す例のように,急速に変化する現象を，短いサンプリング間隔で記録する場合と，長いサンプリング間隔で記録する場合とでは，同じ現象の記録であっても全く別のパターンに見えます．

図0040　正弦波のサンプリングにともなう見掛け上の波．

問　｢これまであまり問題にされていなかった現実の時系列に対する見方が，時系列解析では極めて重要である｣ということを聞きましたが，その｢現実の時系列の見方｣とはどういうことですか？

答　 現実の時系列の見方に次の３つがあります．

この中で(３)は古くから知られ，“ゆらぎ”の原因としてノイズの混入などがありますが，近年の新たな見解では，ノイズ以外にもこうした瞬間的に変動する時系列の重要性が指摘されています．例えば,パルス時系列，矩形時系列，｛1,0}時系列等々で，これらは，正に瞬間的に変動する時系列となっています．これは現実に観測される時系列であると同時に，時系列解析上の評価時系列としても重要な役割を果たしています．
　(２)は近年明らかにされた見方です．これについては問0070で詳しく説明します．
　(１)は最も重要な見方です．これまでの全ての理論体系では，−∞〜＋∞の時系列(無限長時系列)を対象にしているのですが，現実の時系列に適用する場合，現実の時系列の有限性については，これまで全く問題にされてきませんでした．現実の時系列の有限性と解析理論上の時系列の無限性の間のギャップを埋めることが，今後の解析理論に求められています．MemCalcはこれを成し遂げています．

問　｢現実に観測値として得られる時系列データは，必ず離散的で有限長である｣とはどういうことですか？

答　先ず，｢時系列が離散的である｣ということには，次の２つの意味があります．

ここでは，(１)について説明します((２)については，§§3-5 MemCalcの計算精度についてで詳しく述べます)．
　時系列は，ある一定の離散的時間間隔でサンプリングされているために，脳波や血圧脈圧波のように連続的に変動する時系列であっても厳密には連続函数となっていません．血圧のサンプリング間隔30分，１時間あるいは１日で測定する場合は，明らかに離散化の度合は大きくなります．こうした時系列では，サンプリング間隔よりも大きな変動をもつ現象が有意となります．
　次に，｢時系列が有限長である｣ことについて説明します．問0050において触れたように，これまでのスペクトル解析法では，理論構成上，−∞から＋∞の時間領域の時系列(無限長時系列)を前提としています．この前提のために，例えば高速フーリエ変換(FFT)では，時系列データにウインドウ函数などを導入するといった人為操作が不可避となり，結果に様々な問題が生じます．一方現実には，無限の過去から，あるいは無限の未来まで，時系列を得ることは決して有り得ません．これは実際の時系列を見る場合に極めて本質的です．従って，従来の時系列解析を構成する“定常性”や“相関函数”などの定義，更には−∞から＋∞の時間領域の時系列を前提とする理論的体系に対する再検討が必要であり，有限長データが取り扱い可能な解析理論の構築が，今日，求められています．

答　まず，フラクタル(自己相似的)構造について説明します．カオスと密接に関係してしばしば登場する“フラクタル(fractal)”という用語は，“自己相似的(self-similar)”構造を指し示すものとしてベノワー・マンデルブロが造ったものです．こうした構造の具体的な事例は，草木の分岐，河川の分岐，肺や血管の分岐(図0070-1)，土星の輪，放電パターン，表面構造，乱流，分子分光スペクトル等々，自然界の至る所に見つけることができます．例えば，自己相似的構造とは，図0070-1にあるように，心臓血管の網目構造の一部を拡大すると，再び類似の網目構造が観測されるといった構造です．こうしたフラクタル構造をエッシャーが描いています．図0070-2は ｢魚とうろこ｣と題するエッシャーの木版画です．大きな魚のうろこに小さな魚が描かれ，うろこに描かれた魚のうろこにまた魚が描かれる，という具合に，この絵を拡大すると，次々に魚のうろこに描かれた魚の絵が現れます．正に，“自己相似的”に魚が描かれています．

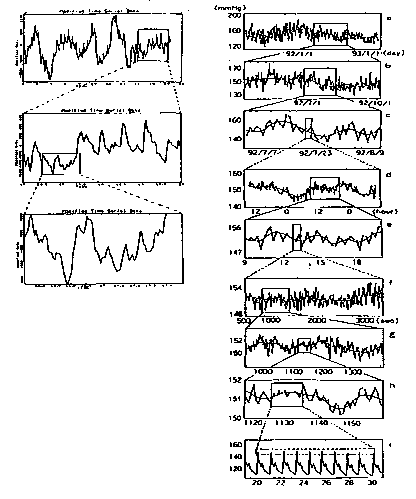
　一般に，構造のフラクタル性は，そのシステムや構成要素の振る舞いのフラクタル性を示します．この具体例は，心臓血管系の構造と血圧や血流の振る舞い，脳神経系の構造と脳波の振る舞いなどに見られます．この場合，構造のフラクタル性とは，心臓血管系については，図0070-1 に示した網状構造であり，構成要素の振る舞いのフラクタル性とは，例えば，血圧や心拍数については，変動時系列に観測される自己相似的構造であり，脳神経系については，その網状構造と脳波時系列の自己相似的構造です．図0070-3に，種々の時間尺度で描かれた脳波の変動時系列，図0070-4に，血圧の変動時系列が示されています．いずれの例でも，時系列の変動パターンは，時間尺度に応じた周期性(リズム)を多重に畳み込んだ構造を示しています．こうのような構造を，自己相似的(フラクタル構造)，あるいは“フラクタル・ダイナミックス”と呼びます．即ち，生体はフラクタル構造となっている多くの異なった構造の器官を有し，それぞれ多くの異なった機能を果たしています．そうした構造に担われた生体の生理学的現象がカオスを示すのです．

問　｢時系列は時々刻々，“瞬間的”に変動する“ゆらぎ”を伴う｣とありますが，時系列に観測される“ゆらぎ”とはどのようなものですか？

答　“ゆらぎ”は，大きな時間スケールの周期的変動の中に重なって観測される小さな時間スケールの変動のことです．この“ゆらぎ”は，決定論的すなわち，周期的あるいはカオス的(非周期的)であれ，非決定論的すなわち無周期的あるいはランダムであれ，時系列に変動を与える源泉です．従って，“ゆらぎ”は対象系の構造や特性を明らかにする上で重要な情報を担っています．しかし，“ゆらぎ”の精確な把握は，理論的にも実験的にも簡単なことではありません．この“ゆらぎ”の振舞いの解明は，統計物理学の中心課題です．

↑ページの先頭へ

↑百問百答目次へ

→　その２(/２)へ