|
答 MemCalcのPSDの計算精度は,MemCalcによって計算される解析結果を理論的解析結果と比較し,その再現性から検証されています.
最初の例として,ローレンツ型時系列は,指数PSDに厳密にフーリエ変換されます.図1290-1(a-1)は,
x( t
) =
1 /
{a2 +
(t -
b)2} |
で a = 1.0,b = 10.0
の場合のローレンツ型時系列です.また,MemCalcによって計算されたMEM-PSDの両対数および片対数表示を,それぞれ,図1290-1(a-2),(a-3)に示します.図1290-1(a-3)のMEM-PSD曲線は,明らかに周波数に対して計算精度の限界で平坦化するまで指数的に減衰していることがわかります.さらに,MemCalcによって計算された指数スペクトルの傾きの値は 12.49であり,理論値 12.56に対してわずか 0.56 %の誤差です.
二番目の例として,指数型時系列
x( t
) =
exp (- a
| t | ) |
は,f
-4のスペクトルの傾きを持つPSDに厳密にフーリエ変換されます.図1290-2(b-1)と1290-2(b-2)に,それぞれ
a =1.0の指数型時系列とMemCalcによって計算されたMEM-PSDの両対数表示を示します.図1290-2(b-2)を見てわかるように,MemCalcの結果は,正確なPSDの結果を良く再現しています.
三番目の例として,ガウス型時系列
は,−α
f 2のスペクトルを持つPSDに厳密にフーリエ変換されます.図1290-3(c-1)にa
=1.0のガウス型時系列,そして図1290-3(c-2)と1290-3(c-3)にそれぞれMemCalcによって計算されたMEM-PSDの両対数表示と片対数表示を示します.図1290-3(c-3)を見てわかるように,MemCalcの結果は,正確なPSDの形を,PSDが現在の計算の精度で決定される限界で平坦化するまで,良く再現しています.
以上のようにMemCalcは,これらの理論的なPSDを再現することを可能にしました.MemCalcによって計算されたこのような結果は,他の時系列解析の方法によっては決して得られませんでした.
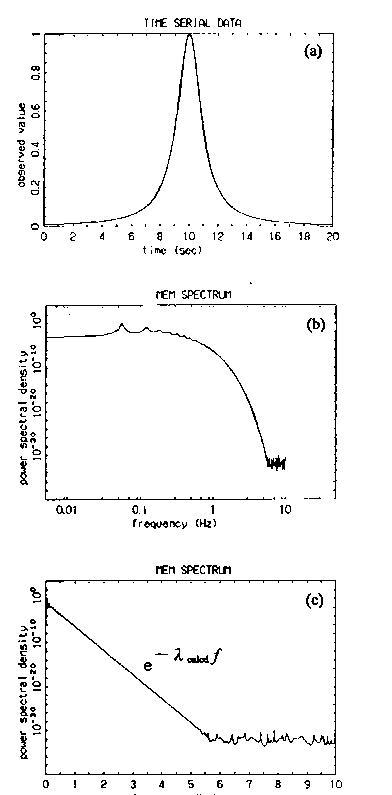
図1290-1 ローレンツ時系列とそのMEM-PSD.
(a)ローレンツ型時系列,(b)MEM-PSDの両対数表示,(c)MEM-PSDの片対数表示.
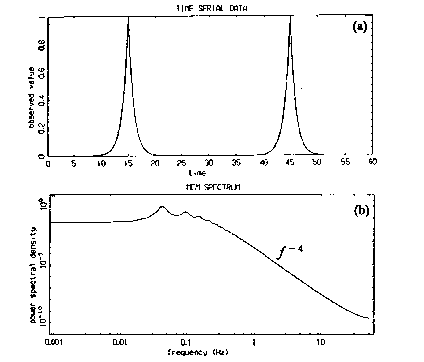
図1290-2 指数型時系列とそのMEM-PSD.
(a)指数型時系列,(b)両対数表示によるMEM-PSD.
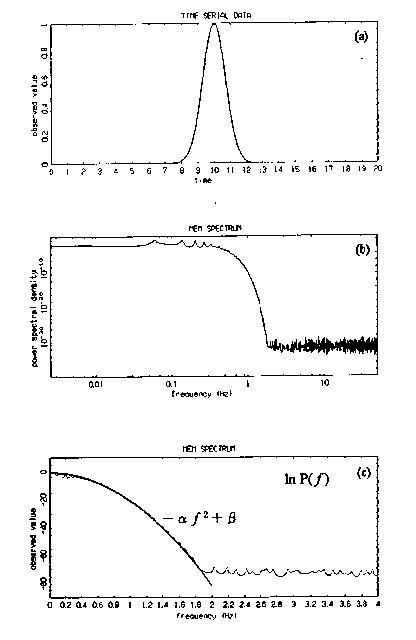
図1290-3 ガウス型時系列とそのMEM-PSD.
(a)ガウス型時系列,(b)MEM-PSDの両対数表示,
(c)MEM-PSDの片対数表示.
|