←　その１(/２）へ

問　解析解のない非線形時系列については，MemCalcのスペクトルの周波数特性の計算精度はどのように検証されますか？

答　私達は，非線形モデルによって生成される時系列をMemCalcで解析することによって，これまで明らかにされていなかった新しい知見を得て，いくつかの論文に発表してきました(参考文献2-2, 2-3, 2-7)．これは，MemCalcの時系列解析法としての類まれなる高精度演算処理で可能となったものです．ここでは，カオス・モデルとして良く知られているレスラー・モデルを用いて，非線形時系列の周波数特性に対するMemCalcの計算精度の検証結果を示します．
　レスラー・モデルは，次式で記述されます．

d x／d t =−y−z，
d y／d t = x＋a y， 　 
d z／d t = b＋x z−c z．

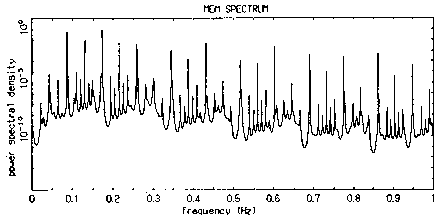
図1320に，a = b = 0.2，c = 4.23 の場合について，レスラー・モデルから得られた時系列に対するPSD曲線を示します．このパラメータ値では，周期的時系列からカオスへの遷移過程にある時系列を発生させることが知られています．図には，基本周波数 f₁ (= 0.1725) をはじめ，非常に多くのピークが存在しています．また，図の顕著なピークの間には，何らかの規則性の存在を予感させます．事実，これらのピークは，基本周波数とその高調波，および基本周波数の分数調波とその高調波に相当する周波数の位置に正確に存在します．この図では，基本周波数に対する４倍までの高調波と，基本周波数の 1/16 までの分数調波とそれらの高調波の存在が明確に確認できます．表1320には，基本周波数までの範囲で観測できる分数調波について，そのピーク位置の周波数値を計算値との比較で示しています．理論値と観測値の誤差の値は極めて小さく，MemCalcが極めて正確な計算結果を与えていることが確認できます．

図1320　レスラー・モデルの時系列データのMEM-PSD．c=4.23の値における時系列データが持つ周期倍加分岐がPSDのピークとして正確に検出されている．

　

表1320　レスラー・モデルによる時系列のMEM-PSDに見られる基本周期とその分数調波と高調波およびそれらの高調波の周波数．

問　MemCalcの周波数分解能はどのようなものでしょうか？それを端的に示す例はありますか？

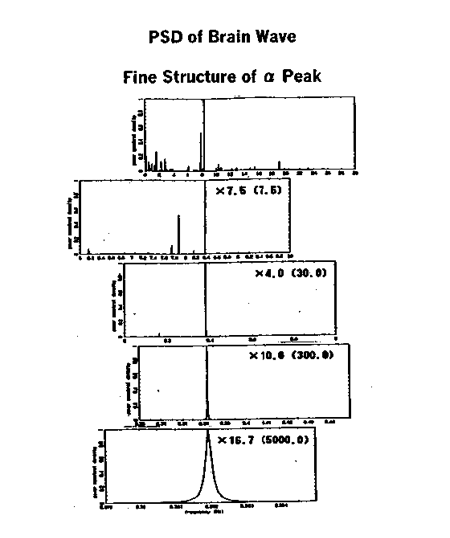
答．図1330に，脳波のα波のスペクトルピークの微細構造を示します．最下図は，αピークの周波数領域を5000倍にしたものです．これは，MemCalcの周波数分解能を示しています．

図1330　(a)脳波のα波のMEM-PSD，(b)(a)の拡大図：7.5倍，(c)(a)の拡大図：30倍，(d)(a)の拡大図：300倍，(e)(a)の拡大図：5000倍．

問　RR間隔(＝拍動間隔)変動データは本質的に不等間隔データです．MEMスペクトルを求めるとき，この不等間隔データを等間隔化する必要がありますが，MemCalcシステムではどのように処理していますか？また，不等間隔データを等間隔化した“修正時系列データ”を詳しく見ると，データごとにサンプリング間隔と最初のデータの観測時刻が異なるようですが．

答　RR間隔変動データに限らず，不等間隔データは次の手順により等間隔化されます．最初に不等間隔の測定時刻を調べ，どのようなサンプリングで等間隔化すべきか，また最初の観測時刻はどう設定すべきかを決めます．それらは一定の評価基準に従い，原データの挙動をもっともよく再現すると思われる値に取られます．次に設定した個々の“観測時刻”の“観測値”を決めるために，前後のデータ点を直線で結び，“観測時刻”から立てた垂線がこの直線と交わる点の高さを“観測値”とします．この手続きはいわゆる直線による単純内挿補間です．
　MemCalcシステムでは以上の手続きに従って，個々のデータごとに等間隔化処理が行われます．従ってデータごとにサンプリング間隔と最初のデータの観測時刻が異なることがあり得ます．

問　等間隔化処理のためにはスプライン補間なども使われますが，なぜMemCalcシステムでは直線による単純内挿補間を採用するのですか？

答　時系列データの変動が従うべき理論式があらかじめわかっているならば，この理論式をもちいて補間すべきです．しかしながら，一般にはそのような理論式は存在せず，存在したとしてもデータの種類ごとに固有のものとなります．それにもかかわらず，例えばスプライン補間やラグランジェ補間などの“高次”の函数を用いて補間することは，その函数のもつ固有の構造をあやまって補間した等間隔データに取り込むことになります．このような点を考慮して，MemCalcシステムではもっとも単純な補間法である直線による内挿補間を採用しています．

問　MEMでは周期性の強いデータの場合にはスペクトル(=スペクトル密度)そのものではなくて，積分値を求める必要があるとういう指摘についてはどうですか？

答　その指摘は，FFTでは周期性の強いデータを(あえて)解析すると，振幅に対応する高さのスペクトルが得られることを想定したものと考えられます．
　理論上，そのようなデータのスペクトルは極めて鋭い(高さが高く巾の狭い)ピークを持ちます．FFTの結果がそうならないのはFFTが周期性の強いデータの解析において破綻するからです．例えば余弦函数のスペクトルは高さ無限大，巾無限小でデータの振幅に応じて一定の面積をもつディラックのδ函数となります．従って，このような場合にはスペクトルの高さで各モードの強弱を論ずることはできず，スペクトル本来の定義に従って各ピークの面積なり周波数帯ごとの面積なりを議論するなどの必要が生じます．
　無限大の高さ，無限小の巾を計算機上で表現することはできません．しかしMEMは周期性の強いデータについてはスペクトルに鋭いピークを持ちますし，特にMemCalcシステムでは計算機の機械精度内で可能な限り，δ函数を疑似的に再現します(問1310参照)．このようなスペクトルについては，理論の示すとおり，面積を議論することが必要です．

問　｢振幅1の余弦函数を用いて発生した人工データのスペクトルをもとめ，そのスペクトルが所定の周波数で高さ１となることを確認したか｣と聞かれました．スペクトルが正しく計算されているならばそのようになるはずだということなのですが，どうでしょうか？

1370

答　周期T，振幅１の余弦函数のスペクトルは周波数1/Tの位置に中心をもつディラックのδ 函数となります(係数0.5が掛かります)．すなわち，高さ無限大，巾無限小，面積0.5となります．ディラックのδ 函数を計算機上に表現することはできませんが，この函数により発生した人工データのスペクトルを計算するとMemCalcでは“疑似δ 函数”とでも呼ぶべき非常に鋭いピークを所与の位置にもつスペクトルを与えます．そしてその面積は理論値0.5に極めて近い値となることが確かめられています．
　“高さ１のスペクトル”とはFFTで計算した際に得られる“スペクトル”ですが，もともとFFTは周期性の強いデータについてはスペクトル解析法として破綻します．したがって，そのスペクトルは理論値とかけ離れたものとなります．ただし，そのような人工データでの結果を検証することは，FFTのプログラムがFFTのアルゴリズムに従って正しく組み立てられているかの検証には使えます(MEMとも，またスペクトル解析法ともなんの関係もありませんが)．

↑ページの先頭へ

←　その１(/２）へ