←　前節(§§３−５)へ

問　MemCalcを最初に適用した成果は，太陽黒点数の時系列データの解析ですが，何故最初に太陽黒点数時系列を解析対象に選んだのですか？

答　太陽は，地球上の人間活動や環境変化に重要な影響をもつために，その周期構造の解明，特に未来の太陽の変動性の予測は，非常に重要です．一方，太陽黒点数の時系列は，しばしば，時系列解析法や予測法の試験データとして用いられてきました．1927年のAR法に基づくYuleの仕事以来，太陽黒点数の変動について多くの研究が為されています．そして，スペクトル法を用いる最近の研究が，BloomfieldやMarpleによって総括されています．これらの研究から，11年周期が，主要な太陽サイクルであると確認されました．しかしながら，Marpleは，｢太陽黒点数データが古典的時系列であるとはいえ，このような比較的短いデータ系列から真のスペクトルを突き止める方法はない｣と指摘し，また，極大の変動する振幅や長期間変化を説明することもできていませんでした．特に，マウンダー極小期(Maunder minimum)の太陽黒点数の変動の異常な振る舞いは，Eddyの報告にもかかわらず，未だに説明されていない問題でした．こうしたことが，現方法を太陽黒点数の解析に適用しようとした私たちの動機です．得られた結果の詳細については，参考文献2-1を参照して下さい．

問　太陽黒点数データの評価はかなり大雑把であると聞いていますが，その精度は問題にならないのでしょうか？

答　ウオルフ(Wolf)の太陽黒点数Rの算出は，次式でなされます：　　　

確かにこの式は極めて大雑把であり，その精度はしばしば問題になっていますが，300年以上の前から，この評価式に従って一貫してデータ集積が続けられている定量的データであり，私たちが長期に渡って入手出来ている貴重なデータです．私たちの解析結果から判断すると，精度の問題を越えて，周期構造を精確に観測できていることが明らかになりました．別の言い方をすると，評価法によるかなりの不確定要素の混入が考えられますが，変動の周期性について見れば，その不確定性を越えて統計的に高い精度が保証されているデータであると言えます．

問　太陽黒点数時系列の解析にあたって，原時系列データの対数変換データを解析対象時系列としていますが，この理由を教えて下さい．

答　太陽黒点数の変動は，平均値を対称軸に見ると，その振幅が平均値の上下にかなり非対称性となっています．こうした変動構造をもつデータをいくつかの基本周期の三角関数波の重畳で表現しようとすると，多くの高調波の混入を避けることができず，基本モードと高調波の区別がつきにくくなります．このために，対数変換することによって，振幅の対称性を高めて解析することが大切な手続きになります．この種の変換としては，対数変換の他に√変換等々，時系列の変動パターンに応じていろいろな変換がとられます．

問　MemCalcによる太陽黒点数時系列解析によって明らかにされた重要な点はどういうことでしょうか？

問　論文�T(参考文献2-1)の成果として，｢太陽活動は本質的にnormalでregularであり，stochasticではない｣としていますが，この根拠と意義は何でしょうか？

答　従来，Maunder極小期の変動(不規則変動)が他の領域の規則性の強い変動と同列において説明ができないために，太陽活動は不規則で予測不能ということが言われてきました．ところが，我々の結果では，このMaunder極小期の特異な変動パターンはその他の規則変動の支配的な領域のデータの延長として説明でき，この結果，太陽活動は予測可能であることが明らかになりました．これに基づいて，論文�Tでは，3000年間の予測を行い，過去の４つの極小期の再現にも成功しました．

問　日単位太陽黒点数データに関する論文�U(参考文献2-5)で明らかになった点はどういうことですか？

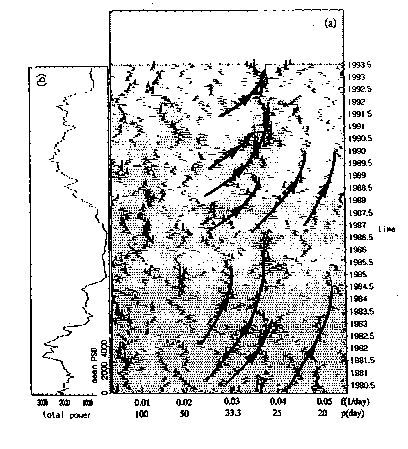
答　最も重要な結果は，図1430の3Dスペクトルに示された太陽自転周期とその多重スペクトル線に相当するスペクトルピークの移動をビジュアルに表示できたことです．即ち，黒点の極側での生成と赤道近傍での消滅と太陽表面の自転速度の違いによる黒点移動の振る舞いが，3Dスペクトル上のスペクトルの推移として明瞭に捕らえられました．

図1430　太陽自転周期とその多重スペクトル線に相当するスペクトルピークの移動．

問　論文�U(参考文献2-5)の成果として，｢太陽活動がdeterministic chaosの可能性が高い｣と言っていますが，これは，先の｢太陽活動は本質的にnormalでregularである｣という見解と矛盾するように見えますが．

答　論文�T(参考文献2-1)では｢太陽の活動は本質的にnormalでregularであり，stochasticでない｣と言っており，論文�Uでは｢PSDの指数減衰性と，subhamonicsの特性から，deterministic chaosである可能性が高い｣と言っています．カオス力学系の特徴は，決定論的であれ，短期予測は可能だが，長期予測は困難である点にありますので，論文�Tと�Uでは矛盾した結論のように思われます．
　しかしながら私たちは，レスラー系を扱った先の論文(参考文献2-3)において，時系列が順カスケードから逆カスケードプロセスを経てカオスに至る複雑なプロセスの詳細なスペクトル解析を行い，明らかにされた周期構造に基づいて，それぞれの状態における時系列の予測可能性について報告しました．そこで明らかなように，順カスケード過程の時系列は基本的に長期予測可能であるが，逆カスケードでは，次第にこの予測可能性が失われ，発達したカオス状態では長期予測不能との結果を得ました．この結果から推測すると，論文�Tの規則性の支配と論文�Uのカオス性の発現とは矛盾するものではないと考えられます．詳しくは，平均太陽黒点時系列の予測可能性について，論文�Uの4.3.3項の記述を参照して下さい．

問　論文�U(参考文献2-5)でいくつかの正弦波を最小２乗法で取り除いた後の残差の振幅のヒストグラムは正規分布に近いを言っていますが，この手続きの意味と意義について教えて下さい．　

答　この手続きは，論文�T(参考文献2-1)で行った“原時系列データの対数変換”と同類の手続きです．データの正規性は良好な解析結果を得るために必要な時系列の基本的特性の一つであると考えられ，その意味で残差時系列は原時系列に比較し，解析対象データとしてよりふさわしく改善されていると考えられます．

↑ページの先頭へ

←　前節(§§３−５)へ