←　前節(§§４−１)へ

問　何故，｢身体現象は，本質的に決定論的であって，確率的ではありえず，しかも非線形である｣のですか？

答　身体現象に限らず，現象の本質を決定論的に見るか，確率論的に見るかは，哲学の分野にも関わる問題です．このことを念頭に置いて，生命現象(身体現象を含め)の本質は系統性と秩序性(規則性，リズム性)にあり，でたらめな状況を回避する傾向が支配的なものです．ホメオスタシスの概念や本能もこういう視点で見るべきものです．その上で，秩序性とは，例えば身体特有のパターン(体形，組織形態，血圧脈圧波や心電波形等々)のことであり，パターンが形造られること自体，あらゆる点で非線形なものです．例えば，外皮による身体と外界との区別，心電波形など，特有のパターンが周囲と明瞭に区別されるのは，周囲から線形・連続に変化するのではないからです．

問　『｢身体の非線形性｣を単純なモデルに基づいて安易に解釈する傾向がある』とありますが，実際の現象を理解しようとするときには，まず単純なモデルを組み立て，実際の現象と比較し，モデルをより現象に近づけるために改良・発展させていくのが常道ではないでしょうか．一体，これまでの｢身体の非線形性｣のためのモデルの研究では，何が問題であったのでしょうか？

答　｢身体の非線形性｣については更に述べるまでもなく，明白なことですが，この身体現象を｢単純なモデルで表現する｣と言ったとき，一般には２つの取り扱いになります．一つは，線形モデルで表現すること，他の一つは比較的単純な非線形モデルで表現することです．この２つに共通した問題点は，複雑で多様な対象構造と現象の一部分を定式化しているに過ぎないことにあります．非線形現象が支配的な系においては，部分と全体とが関連をもって存在しており，部分を表現するためには全体の知識が必要であり，全体は部分の集合体で説明できないということが起こります．このために，部分表現をいくら積み重ねても(改良・発展させても)，真の現象を記述することはできません．例えば，認知といった極めて高度の脳活動現象を限られた情報(部分情報)に基づいて定式化しても，その結果は単なる部分的現象論的説明にしかすぎないものです(Bogoljubov ｢非線形振動論−漸近的方法｣参照)．この決定的とも言うべき限界を見ない研究者が多いのも事実です．また，心臓の秩序を定式化する多くの研究が行われ，今日のコンピュータの計算能力の拡大と歩調を合わせて，次々に新たな非線形項が加わった複雑な方程式へと進んでいますが，非線形項は一つでも入っているだけで，解析し難い問題が生じます(この例は，ロジスティック方程式を解くことを見れば明らかです)．このことは，非線形現象を単純に扱う場合の本質的問題点を示しています．

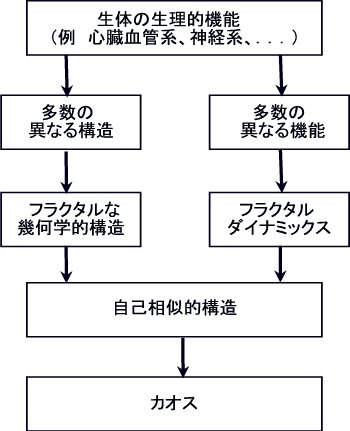
問　近年，生体の生理現象が“カオス”と“フラクタル”の視点から議論されています．生体の生理現象のカオスおよびフラクタルの関連とはどのようなものですか？

答　一般に，構造のフラクタル性は，そのシステムや構成要素の振舞(例えば時系列として観測される)のフラクタル性を示します．これは，今日，カオス現象として，基礎から応用まで極めて広範囲に研究されて，カオスに関係した発表論文数も膨大な数になっています．例えば，"Bibliography on Chaos"(World Scientific，1991年刊)には，1990年末までに7000を越えるカオス研究に関連した研究論文の表題を収録しています．とりわけ，生体におけるカオスは，多くの学問的興味の対象となっているだけでなく，カオス利用技術の開発にも多くの貴重な知見を与えています．
　生体における“カオス”は一般に次のように説明できます．即ち，生体は多くの異なった構造の器官を有しており，それぞれ多くの異なった機能を果たしています．それらの構造は，“フラクタル構造”となっており，その構造に担われた生体の生理的現象は，“フラクタル・ダイナミックス”となります．こうして生体の生理学的現象は“カオス”特性を示します．この概略を図1480に示します．この描像は生体に限らず，自然現象一般にもそのままあてはまります．しかし，何をもって“カオス”とするかについては，多説があって正に“混沌”としています．また従来の定義は，有限長の現実の観測デ−タのカオス性を検証するには殆ど役に立ちません．こうした状況にあって，私たちは，最近，短い時系列からでもカオス性を定量的に指し示すことのできる幾つかの特性を明らかにしました．私たちが見出したカオスの特性については問1500を参照してください．

図1480　生体の生理学的現象の“カオス”特性の概略．

問　生体の生理現象のカオスおよびフラクタルを示す例として，これまでどのようなものが知られていますか？

答　問0070を参照して下さい．

問　これまで，血圧脈圧波はカオス特性を有することが多く報告されていますが，MemCalcでは，血圧脈圧波のカオス特性についてどのような指標を明らかにしましたか？

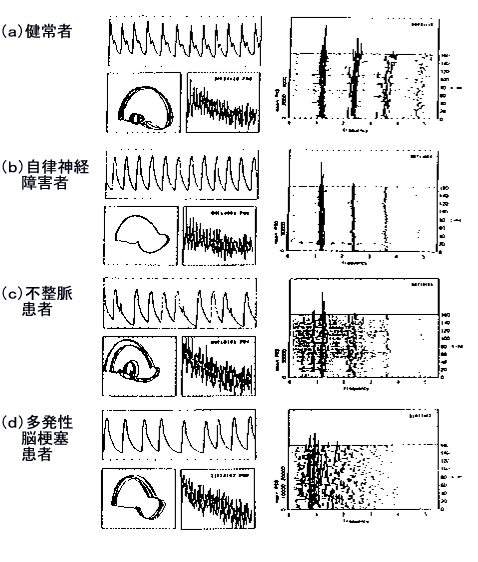
　図1500は，(a)１人の健常者と３人の疾患者((b)自律神経障害者，(c)不整脈患者，(d)多発性脳梗塞患者)の血圧脈圧波の時系列データ(左上)と，それぞれのトラジェクトリー(左下左)，PSD(左下右)および3Dスペクトル・アレイ(右)を示します．
　まず，“�@PSDが低周波数領域を除き，全体として指数スペクトルを示す”についてですが，図1500の左下右のPSDを見てわかるように，いずれの時系列についても，PSDは疾患に関係なく指数型となっています．このことは，血圧波動の背後に決定論的力学過程が存在することを強く示唆します．
　次に“�A基本モードと高調波が確認される”についてですが，図1500の右の3Dスペクトルアレイをみてわかるように，心拍サイクルに対応する基本モードとその高調波に対応するスペクトル・ピークが，3Dスペクトル・アレイに明瞭に見られます(多発性脳梗塞患者を除く)．不整脈患者の場合については，不整脈は不規則であると考えられていますが，不整脈のスペクトル・アレイは，その周波数が基本モードと違っているものの，規則的な振動構造を持つことが分ります．�Bと�Cについては，更に検討が必要です．これは問1510で説明します．

図1500　血圧脈圧波の解析結果．ａ：健常者，ｂ：自律神経障害者，ｃ：不整脈患者，ｄ：多発性脳梗塞患者．それぞれの対象について，(左上)血圧脈圧波時系列，(左下左)トラジェクトリー，(左下右)PSDの片対数表示，(右)3Dスペクトル・アレイ．

問　血圧波動のカオス性の判定はどうすればわかりますか？

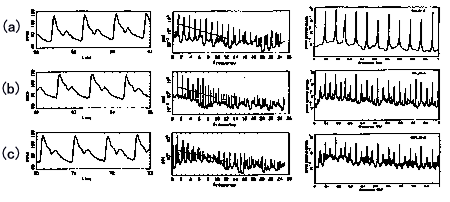
答　血圧波動が本質的に決定論的力学系に基づいていることは疑いのないことですが，血圧波動がカオス的であるのか，あるいはそうでないのか，を解明するために，血圧波動が問1500で述べた�Bと�Cの特徴を持つか否かが重要となります．図1510は，健常者の血圧波動の３つの連続する時間領域((a)58〜61秒，(b)62〜65秒，(c)70〜73秒)の時系列(左)と，それぞれのPSD(中)ですが，これを同図の右に示してあるカオスモデルとして有名なレスラー・モデルの結果と比較して見ると以下の興味深い事実が明らかになります．即ち，(a)の結果は，基本モードと高調波に対応するスペクトル・ピークが観測され，これはレスラー・モデルの周期的解に相当します．(b)の結果は，基本モードと高調波に加えて，分数調波の成長が観測され，これはレスラー・モデルの周期倍分岐過程で見られるものに相当します．そして，(c)は，レスラー・モデルの逆カスケード過程で見られたものに相当します．こうした結果は，健常者の血圧変動について，カオス現象を特徴付ける周期倍分岐過程と逆カスケード過程の確認ができることを示すだけではなく，その血圧変動のカオスは，ある状態から別の状態へ，レスラー系について言えば，制御パラメータ値で決まる種々の状態に，複雑に遷移するといったものであることを示しています． 自律神経障害者の場合に，こうしたカオス性を見いだすことはできません．

図1510　(左)連続する時間領域における血圧脈圧波時系列，(中)そのPSDの片対数表示,(右)レスラー系のパラメータc＝3.5(右上)，4.1(右中)および 4.30(右下)に対するPSDの片対数表示．血圧脈圧波時系列のPSD(中)には，レスラー・モデルについて観測された分数調和波(周期倍分岐)やその消滅(逆カスケード)が見られる．

問　各血圧脈波の3Dスペクトルアレイはそれぞれ振舞いが異なりますが，PSDの傾きはいずれの場合も指数的です．各血圧脈波の周波数構造の違いは，スペクトルの形状に現れないのでしょうか？

答　ここで重要なのは，指数の係数の値(PSDの傾きλ)です．表1520に，各血圧脈圧波のλ値をまとめてあります．

表1520 10秒間の血圧脈圧波に対する
MEM-PSDの傾き(λ).

自律神経障害者が４例中最も大きく，健常者と多発性脳梗塞患者とが，最も小さく，ほぼ同じ値になっています．問0390の図0390-2でレスラー・モデルについて見たように，決定論的力学系から生成される周期的非線形波動では，もしゆらぎの影響が小さければ，高周波数成分が速やかに減衰し，傾きの大きさλの値は大きくなります．自律神経障害者が４例中最も大きい理由はこの場合に相当していると考えられます．一方，決定論的力学系に作用するゆらぎに関しては，２つの場合が考えられます．一つは，決定論的過程に確率的性質が付加されているように振る舞う場合です．この場合の確率的性質は，系の非線形性による不安定性によって生み出される振幅ゆらぎに起因するか，あるいは，ランダムなノイズの混入によるか，によってもたらされます．こうしたゆらぎが支配的である場合，高周波数成分は速やかに減衰せず，λの値は小さくなります．健常者と多発性脳梗塞患者の時系列のλ値は，最も小さく，ほぼ同じ値であるという結果は，それぞれ，健常者の場合は振幅ゆらぎによる結果と考えられるし，多発性脳梗塞患者の場合は，(恐らく，内因性の)ランダムなノイズ的擾乱の混入の結果であると考えられます．

答　非線形力学過程は，周期状態から倍周期分岐，逆カスケード状態(カオス状態)に至るあらゆる状態を呈示しますが，その全ての状態のPSDは指数特性を示します．従って，指数PSDが必ずカオス状態に対応するとは限りません．また，3Dスペクトルアレイの周波数ゆらぎがカオスに起因するものかどうかは，それだけでは判定できません．このようなことから，PSDの結果のみからカオス性を判定することは，一般にはできません．良く知られているリアプノフ指数についても，非カオスでも正になることは良くありますので，万能ではありません．

問　血圧脈圧波の他に，MemCalcによってカオス特性が確認された生体時系列にはどのような例がありますか？

答　生体時系列は，全てカオス特性を示すを考えられますが，MemCalcを適用した例は，今のところ血圧脈圧波，脳波そして感染症発生数時系列データに限られています．脳波は，フラクタル構造が確認されますので，十分カオス性が見いだされるはずですが，カオスの指標�Bと�C(問1500参照)の特徴を引き出すには成功していません．これは精度など脳波の計測そのものの問題があります．感染症発生数時系列データについては，麻疹データに典型的にカオスの指標�@〜�C(問1500参照)が確認されました．この点については，問1550を参照してください．

↑ページの先頭へ

←　前節(§§４−１)へ