| §4 実データのMemCalcによる解析 |
||||
| §§4−2 生体時系列(その2) |
||||
|
問 感染症発生数時系列データにMemCalcを適用する意義を説明して下さい.MemCalcはとりわけそのカオス特性を調べるために活用できると聞きましたが,カオス性についてどのような結果が得られましたか? |
1550 |
|||
|
答 周期的流行を示す感染症(特に麻疹)の発生変動の時系列は,決定論的力学モデルの対象として数理学的に研究されて来たましたが,今日,カオス研究の格好の対象ともなっています.しかし,最もデータの蓄積がなされているニューヨーク市のデータで,500ケ月であり,「信頼できる解析には,いまひとつデータ不足である」とR.メイによって指摘されています.従って,短い時系列データからカオス性についての情報を引き出す方法が求められていました.血圧脈圧波に適用した私たちの方法(問1500参照)は,こうした短いデータからカオス性を引き出すことに一定の可能性を与える方法です.
結果の詳細については,参考文献2-6を参照してください.
|
||||
|
問 麻疹データのPSDの時間変動は,データに混入するノイズによるものであるとは考えられませんか? |
1560 |
|||
|
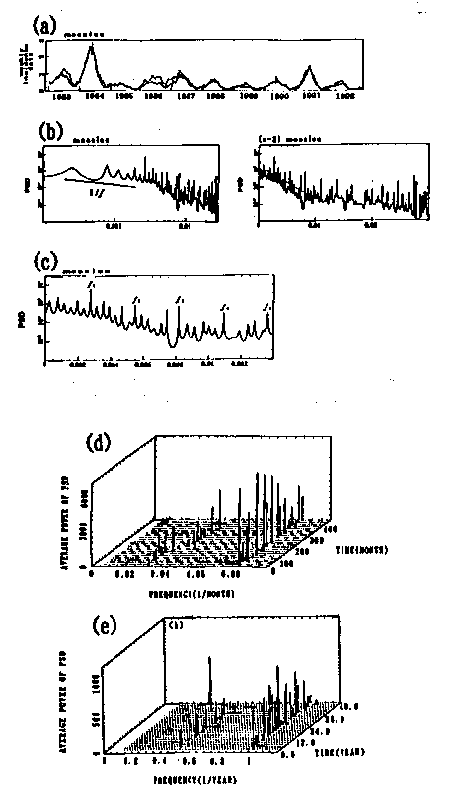
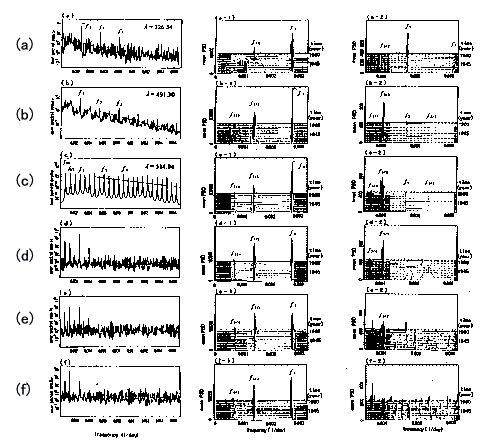
答 図1560は,麻疹データの場合に観測される周波数揺らぎがカオス性によるものであるか否かの検証を行った結果です:(左)PSD,(中)低周波数領域の3Dスペクトルアレイ,(右)高周波数領域の3Dスペクトルアレイ.(a)図の現実の麻疹データと(b)図のSEIRモデルによるカオス時系列についての結果を見ると,両者の場合とも,PSD((a)図と(b)図の左)で指数スペクトルと連続成分が観測され,そして低周波数領域の3Dスペクトルアレイ((a)図と(b)図の中)では分数調波のゆらぎが観測されます.このことから,麻疹発生変動がカオス過程であることが推測されます.
図1560 麻疹の時系列データのカオス過程の検証.(左)PSD,(中)低周波数領域の3Dスペクトルアレイ,(右)高周波数領域の3Dスペクトルアレイ.(a)ニューヨーク市で報告された麻疹データについて,(b)SEIRモデルによるカオス時系列について,(c)SEIRモデルによる周期的時系列について,(d)周期的時系列に10%レベルのノイズを付加した時系列について,(e)周期的時系列に20%レベルのノイズを付加した時系列について,(f)周期的時系列に50%レベルのノイズを付加した時系列について. |
||||
|
問 麻疹の発生メカニズムがカオス的であると解明されたことが,予防医学上,どのように役立つと考えますか? |
1570 |
|||
|
答 麻疹の発生メカニズムがカオス的であるという知見は,実際の麻疹データについて行った解析結果と,麻疹発生の非線形数理モデルから発生されるカオス時系列の解析結果が本質的に一致することから得られました.麻疹の数学モデルでは,未感染者の数がある一定数以上存在し,かつ,夏休みや冬休みに子供たちが物理的に接触を持つ機会が少なくなる,即ち,感染率が一年周期で変化するという条件が満たされることによって,麻疹の流行が発生することが説明されます.このことから,麻疹の流行を食い止めるためには,流行を支配する要因に影響を与えるような対策を興じる必要がある,という知見が得られます.このように,観測データの限られた知見を超えて,非線形数理モデルによる系統的・総合的解析への道を開くことが可能になります. |
||||
|
問 生体時系列で3Dスペクトルアレイから新たな医学診断上の知見を得られた例はありますか? |
1580 |
|||
|
答
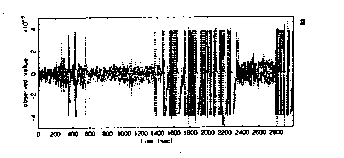
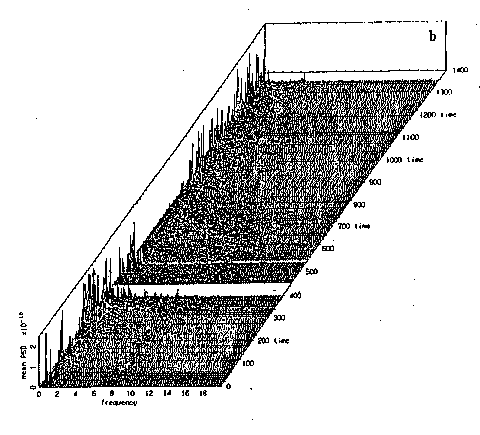
図1580は,手術中,麻酔導入時からの脳波の変動を調べた結果です.脳波時系列(上)は,サンプリング間隔20ミリ秒で1300秒にわたって得られています.部分的に脳波の振幅が振り切れているのは,電気メスによる処置などが行われているためです.この時系列をセグメント時系列解析し,得られた3Dスペクトル・アレイ(下)から,次のような状況が見てとれます.0〜200秒にかけて,周波数8Hz付近にα波が観測されます.その後100秒位の間は,α波が消失し,代わりにδ波(4Hz以下)が隆盛になります.これは麻酔効果と見られます.300〜500秒間は,δ波がやや弱まり,4Hzから14 Hz辺りまでピ−クが広く分散するようになります.500〜800秒の間は,δ波が殆ど消失し,スペクトル・ピ−クが周波数の全域に分散し,一部は18
Hz付近に及びます.この状況は,この間に行われた処置によるものであると判断されますが,詳しい因果関係はわかりません.その後再びδ波は隆盛になり,スペクトル・ピ−クも低周波数領域に集中するようになります.このように,手術中の脳波の時々刻々の変動を通して,患者の状況が的確に把握できることがわかります.
|
||||
|
問 MemCalcで睡眠・覚醒リズムを解析した結果のPSDの特徴にはどのようなことがありますか? |
1590 |
|||
|
答 系の,おそらくは周期的であると思われるさまざまな挙動を明らかにするために,系の状態を反映すると考えられる複数の種類のデータを観測するとします.例えばヒトの睡眠・覚醒リズムであれば,被験者のおかれたさまざまな状況を勘案して,最も簡単には入眠・起床時刻の記録のみをおこなって覚醒時を値1,睡眠時を値0として,30分ごとに0,または1の並んだデータを得ます.これは矩形波時系列データであり,得られるスペクトルは高調波の影響が強いスペクトルとなります.他方,状況によっては1分ごとの深部体温のデータを測定できることもあります.ともにヒトの1日のリズムを見たいわけですが,共通点もありますが,両者のスペクトルの様子は大分異なっているように思われます. |
||||
|
問 心電位変動を観測して拍動間隔のゆらぎを取り出します.24時間程度のデータを解析すると,そのスペクトルにはおおくの場合に約24時間の逆数の周波数位置に顕著なピークが,そして約12時間・約8時間の逆数の周波数位置などにもピークが得られます.さて,10日間のデータを解析したところ,加えて約7日・約3.5日の逆数の周波数位置にもスペクトルピークが現れました.これら2系列のスペクトルピークをどのように考えるべきでしょうか? |
1600 |
|||
|
答 24時間データについて観測される24時間の逆数の周波数位置のピークは,データ長の影響の可能性もあると考えられますが,24時間のリズムを反映している有意なピークと判断されます.12時間,8時間の逆数の周波数位置のピークは,24時間リズムの高調波とも考えられますが,被験者の社会生活のリズムを反映している可能性もあります. |
||||
|
問 矩形波データのスペクトルは相当に特殊な振る舞いをすると考えられます.例えば上述の睡眠・覚醒リズムであればそのスペクトルでリズムの本性をを直接に反映している特徴はどのようなものでしょうか.また,矩形波データに特有の,スペクトルに必然的に含まれる特徴はありますか? |
1610 |
|||
|
答 矩形波データに特有なスペクトル上の特徴は,高調波の混入が多いことです.また,矩形波と言っても,睡眠・覚醒リズムのような場合,不規則性が著しいもので,この結果はスペクトルピークの幅の広がりとして現れます. |
||||
|
問 30分ごとに約1日にわたり測定した血圧データ(ABPMデータ)をMemCalcで解析してその基底変動(日内リズム)を検討し,約24時間の周期を見いだしました.ところが,「24時間の周期を検出するためには48時間の測定長が必要であり,従って測定が約1日では結果は信用できない」と主張される先生がいました. |
1620 |
|||
|
答 結論からいいますと,その先生の主張はFFTに関しては正しいのですが,MEMないしスペクトル解析一般の立場からは誤りです.FFTは特に低周波領域での分解能が悪く,この領域を問題とする場合にはデータ長を充分に長くとることが必要です.FFTである周期のリズムをみるためにはデータ長としてその2倍以上必要であるというのは,FFTをさまざまなデータに適用して得られた経験上の重要な知見です. MEMは短いデータ長からも低周波数帯を含めて分解能の高いスペクトルを計算できることが特長ですが,例えば,MemCalcシステムではデータによっては観測期間の5〜10倍に相当する周波数帯にピークが現れ,かつ,このピークの示すモードを取り込むことにより,原時系列データに対するあてはめが相当改善する例があります. |
||||
|
問 ABPMによる血圧測定と解析では,よくその日内リズムの再現性が問題となります.同一の被験者について複数回の測定を行い,その基底変動のトラジェクトリーを描いたところ,まったく異なるものとなりました. |
1630 |
|||
|
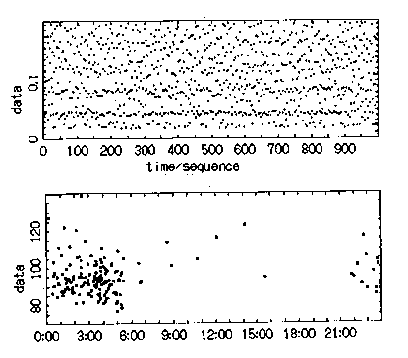
答 同一の被験者についての複数のABPMデータの基底変動のトラジェクトリーが互いにまったく異なる点ですが,データを解析した結果,“トラジェクトリーで問題とするような詳細なレベルで血圧変動を捉えると,その変動パターンは同一の被験者でも日々大きく異なっている”と結論されます.もちろん,健常者の血圧は昼間高く,夜間に低いという明確な日内変動を示しますから,日々ごとに大きくことなる血圧変動パターンにも必ずそのような日内変動の特徴が含まれることが期待できます.図1630は約170例の健常者を主体とする集団についてABPMによる測定を行い,MemCalcシステムで解析し,その結果をまとめたもので,(a)がスペクトルのピーク周波数の分布を,(b)が基底変動の最小値とその時刻の分布を示したものです.(a)より血圧変動を構成する個々のリズムの周期は48時間,24時間,12時間,8時間などに中心をもつことが,また,(b)よりそれらのリズムが重畳して血圧の基底変動を構成するとき,午前3〜4時に最小値をもつことが示されます.同様の結果は,おそらく同一の被験者の多数回の測定の結果からも得られると考えられます.
|