| ���S�@���f�[�^��MemCalc�ɂ���� |
||||||||||||||||||||||||||||||||||
| �����S�|�R�@����`�E�J�I�X���n��(���̂P) |
||||||||||||||||||||||||||||||||||
|
��@���n��f�[�^���ϑ�����ړI�͂��̃f�[�^�������n�̏�ԂɊւ���m���邱�Ƃɂ���܂��D���̏�ԂɊւ��Đ��`�V�X�e���Ƃ��錾�t���܂��D���`�V�X�e���Ƃ͉��ł����D |
1640�@ |
|||||||||||||||||||||||||||||||||
|
���@����V�X�e�������݂���Ƃ��C���̎��ԓI�E��ԓI���W(�ω�)�͒ʏ�����������ŕ\���ł��܂��D�Ⴆ�C���ԕω����L�q��������������ɂ��āC��������(t = 0 �̂Ƃ��̒l)��^����ƂP�̉������܂�Ƃ��C�قȂ鏉�������̉��Ƃ̊Ԃɏd�ˍ��킹�̌�������������Ƃ��C�������`�V�X�e���ƌĂ�ł��܂��D�Ⴆ�C���`�V�X�e���ł͏��������Ƃ��� t = 0�ŏ����l A(1)�̏ꍇ�ɉ��P�CA(2)�̏ꍇ�ɉ��Q�CA(3)=A(1)+A(2)�̏ꍇ�ɉ��R��Ƃ��C���R= ���P+ ���Q�ƂȂ�C���̂悤�ȊW���d�ˍ��킹�̌����ƌĂт܂��D�܂��C����V�X�e���ɑ�����͂Əo�͂̊W�����W�ɂȂ��Ă���ꍇ�C���̃V�X�e������`�V�X�e���ƌ����܂��D�Ⴆ�C�g�o�l�̐L�� y (�o��)��������ꂽ�� f (����)�ɔ�Ⴗ��h�Ƃ����t�b�N�̖@��(Hooke's law)�C y = k f �G k : ���萔 |
||||||||||||||||||||||||||||||||||
|
��@�킽�������Ɏ���ɁC�ǂ̂悤�Ȑ��`�V�X�e��������܂����H |
1650 |
|||||||||||||||||||||||||||||||||
|
���@���B�̎���Ɍ����Ȑ��`�V�X�e�������o�����Ƃ͓�����̂ł��D��1640�ŏq�ׂ��o�l�̐L�тƗ͂̊W�ɂ��Č���ƁC�o�l��������x�ȏ�L���ƁC���`�V�X�e���̓����ł�����͂Əo�͂Ƃ̊Ԃ̔��W��������Ă��܂��܂��D���̂Ƃ����͂���`�V�X�e���ł͂Ȃ��Ȃ��Ă��܂��܂��D�Ƃ���ŁC���W����������L�т͈̔͂ɂ��Ă��C�o�l�̔��萔�͌����Ɍ���ƁC���x��o�N�ω��ň��l���Ƃ���̂ł͂���܂���D���̂悤�ɁC�V�X�e�����Ƃ�܂��O�I�v����V�X�e�����g�̓��I�v���ɂ���Ĉꌩ���`�V�X�e���Ɍ����Ă��Ă��C�����ɂ͂����Ȃ��Ă��Ȃ��̂����B�̐g�̎���̃V�X�e�����ƌ����Ă�����������܂���.����͐g�̎���̃V�X�e�������l�ȗv�f���܂ޕ����I���݂ł��邩��ł�. |
||||||||||||||||||||||||||||||||||
|
��@���`�V�X�e���ɑΔ䂳���T�O�Ƃ��Ĕ���`�V�X�e��������ƕ����܂����D����`�V�X�e���Ƃ͉��ł����H����`�C����`�������Ƃ͉��ł����H |
1660 |
|||||||||||||||||||||||||||||||||
|
���@����`�V�X�e���Ƃ́C��1650�̗�ɂ��Č����C���̏d�ˍ��킹�̌������������Ȃ��V�X�e���C���邢�́C���͂Əo�͂̊W�����W�ɂȂ��V�X�e���̂��Ƃ��Ӗ����܂��D��ʂɁC���R�E�͔���`�V�X�e���ł���C���ꂪ�悷�錻�ۂ͖{���I�ɔ���`���ۂł��D�Ⴆ�C����`�V�X�e���Ƃ��ėǂ��m��ꂽ���X���[�n��[�����c�n�́C�����̕������ŋL�q����܂��D �@
�����ŁCX�CY�CZ
�͕ϐ��Ca�Cb�Cc�C���C��
�͒萔�ł���C����`���̓��X���[�n�̏ꍇ�͂P�̔���`��XZ�C���[�����c�n�̏ꍇ�͂Q�̔���`��
XY
��XZ
�ɂ���Đ��N����܂��D���̂悤�ɕϐ��̐ς̍����������������`�������ƌĂт܂��D |
||||||||||||||||||||||||||||||||||
|
��@���ۂɂ͂ǂ̂悤�Ȕ���`�V�X�e��������܂����H����`�n�����肵�đ��݂�����������͂ǂ̂悤�Ȃ��̂ł����H |
1670 |
|||||||||||||||||||||||||||||||||
|
���@�����ɑ��݂���V�X�e���́C���̎��ӊ��Ɖ��炩�̑��ݍ�p���Ă���C���̂��߂Ɉ�ʂɂ͔���`���ۂ������̂��ʗ�ł��D�Ⴆ�C�l���݂̒���������Ƃ��l���Ă݂�ƁC���荞�ނ��Ƃɂ���ėאl��O���̐l�ɉe�����y�сC���X�ɂ��̉e�����L�����Ĉ��̔z�u�ɂȂ�܂��D���ɁC�O�����痈��l������C�אl�̉e�����Đi�H�����܂�C���̕����ɕ��݂�i�߂邱�ƂɂȂ�܂��D���̌��ʁC�܂��e�������ӂɋy�сC���̎��ӂ���̍S�����i�H�����܂�܂��D���̂悤�ɁC���ӂƂ̑��ݍ�p���J��Ԃ��Č��ۂ����W���܂��D���̂悤�Ȍ��ۂ͌����Đ��`���ۂƂ��ċL�q���邱�Ƃ͂ł��܂���D |
||||||||||||||||||||||||||||||||||
|
��@����`���ۂ̋�̗�������Ă��������D |
1680 |
|||||||||||||||||||||||||||||||||
|
���@���B������I�ɖڂɂ�����̂͑S�Ĕ���`�V�X�e���ł���ƌ����Ă����̂ł��D�Ⴆ�C�K�����C�������C�������C���������������̂́C���ԓI�ϓ��ł���C��ԓI�ϓ��ł���C�S�Ĕ���`���ۂł��D���ɁC������Ƃ���ɒ����������邱�Ƃ��o���鐶�����ۂ͔���`���ۂ��̂��̂ł����āC���Ɂg������h���Ƃ�����`���ۂȂ̂ł��D�S���̔���(�����I���Y���`��)�C�����܂��Ⴍ�����J�G���ɂȂ�(�`�Ԍ`��)�C�g�J�Q�̃V�b�|�������ւ��(���ȏC���@�\)�Ȃǂ͔���`���ۂ̓T�^�ł��D���镔�������ӂƎ��ʂł���(�p�^�[���`��)�Ƃ������Ƃ́C�����ɓˑR�ɋ}�s�ȕω�������邱�Ƃł���C���������`���ۂł��D |
||||||||||||||||||||||||||||||||||
|
��@�����ɑ��݂���V�X�e���͐��`�V�X�e���Ɣ���`�V�X�e���̓�ɕ��ނ��邱�Ƃ��ł���̂ł����H |
1690 |
|||||||||||||||||||||||||||||||||
|
���@�����ɑ��݂�����̂́C�S�Ĕ���`��{���Ƃ��Ă��܂��D�]���āC���`�n�Ɣ���`�n�ɕ��ނ��邱�Ƃ͏o���܂���D�B��C���ۂ̓��́|�o�͂̊W������Ƃ��C���̊W�����`�W(���W)���炸�ꂪ�������ꍇ�ɂ̂݁C���̌��ۂ������n����`�n�Ƃ݂Ȃ��܂��D����́C�����܂ł��g�݂Ȃ��h�Ƃ������Ƃł����āC���̌n�����`�n�ł���Ƃ������Ƃł͂���܂���D���̂悤�ɁC���`�n�͋ɂ߂Č��肳�ꂽ���ʂ̏ꍇ�ɂ݈̂ꌩ�����g�݂Ȃ���h�Ƃ������̂ł��D����܂ŁC�����̈���n�͐��`�n�ł���ƍl�����Ă��܂������C����͐��`�Ƃ��Č��Ȃ���Ή�͂ł��Ȃ��������߂ł����D |
||||||||||||||||||||||||||||||||||
|
��@���̕\����ڂɂ��܂����D�����`���ƕ��G���̉Ȋw�I�w�W�E������܂��Ɋm������Ă��Ȃ���D���̊m������Ă��Ȃ����R�͉��̂��ƍl���܂����H |
1700 |
|||||||||||||||||||||||||||||||||
|
���@����`���̉𖾂́C����Ȋw�̏d�v�ȉۑ�ł����C���݂̂Ƃ������`�������܂˂��𖾂��邱�Ƃ͖w�Ǖs�\�ł��D�܂��C����`���ۂ͋ɂ߂đ��l�ł���C�����������ۂݏo���V�X�e���͑��d�\��(�t���N�^���\��)�ł���C�����ƑS�̂��邱�Ƃ��o���܂���D���̂悤�ȃV�X�e���͕��G�n�ƌĂ�܂��D�]���āC���G���́C������𖾂��邱�Ƃ͕s�\�ł��D�������Ĕ���`���ƕ��G���̉Ȋw�I�w�W�E��͍������Ċm���ł��Ă��܂��C�{���I�ɍ���Ȃ��̂ł��D�Ⴆ�C�g�̌��ۂ́C�{���I�Ɍ���_�I�ł����āC�m���I�ł͂��肦���C����������`�ł��D���������̂��Ƃ���̓I�ɉ𖾂��邱�Ƃ͂����ȒP�Ȃ��Ƃł͂���܂���D����́C�܂��ɐݖ�ɂ���悤�ɁC�g�g�̂̔���`���h���{���I�Ɂg���G���h�ƊW���Ă��邽�߁C���̉Ȋw�I�w�W�E������܂��Ɋm������Ă��Ȃ����߂ł��D����́C�Ⴆ�C�g�̌��ۂ́g�J�I�X�h�̒�`�̍�����݂�Ζ��炩�ł��D�ɂ�������炸�C�߂������`��͂Ƃ��J�I�X��͂Ə̂��āC�g�g�̂̔���`���h��P���ȃ��f���Ɋ�Â��Ĉ��Ղɉ��߂���X���������܂��D���������X���́C�\�����܂��߂邱�Ƃ��K�v�ł����C�����ꂻ�̖�肪���炩�ɂȂ��āC�����������ՂȌX���ɏI�~�����ł���邱�ƂɊԈႢ����܂���D |
||||||||||||||||||||||||||||||||||
|
��@����`�V�X�e������͂�����@�ɂ��Đ������Ă��������D��͕��@�̑Ó����̌��͂ł���̂ł��傤���H |
1710 |
|||||||||||||||||||||||||||||||||
|
���@���̂Ƃ���C����`���ۂ̉�͂́C���ۂ����f������������`�������𗧂āC������������ƂŐi�߂��܂��D��������͉���������̂́C�����܂�ȓ��ʂȏꍇ�Ɍ��肳��C�قƂ�ǂ̏ꍇ�C���l�v�Z�ɂ���ĉ������߂邱�Ƃʼn�͂��s���Ă��܂��D�����ɂQ�d�̍���t���܂Ƃ��܂��D���́C���f�����ǂ��܂œK���C�����̌��ۂ��ǂ��܂ŕ\�����Ă���̂��Ƃ������ł��D����`�n�́C�����E�v�f�ɕ����E���͂��C������ĂяW�߂đS�̂��\������Ƃ����C���`��͂ŋ�������@���Ƃ邱�Ƃ��ł��܂���D�S�̂����f��������ɂ͑S�̂𗝉��ł��Ȃ���Ȃ�Ȃ�����ł��D�������l�Ԃ̔F���ɂ͌��E������C�S�̂𗝉����邱�Ƃ͕s�\�ł��D�������āC���f���͔���`�n�̈ꕔ�̕\���ɉ߂��܂���D���̍���͔]�̃��f�����ɂ��̓T�^����݂邱�Ƃ��ł��܂��D���́C����`�������𐔒l�v�Z����ꍇ�́C������(���U��)�C�����l�ˑ����C�v�Z�A���S���Y���ɂ��덷�C�����ėݐό덷�������炷�s��I��肪����܂��D�������Ĕ���`���ۂ𐔗����f���Ŏ�舵�����Ƃɂ͏d��Ȍ��E������ƌ����܂��D |
||||||||||||||||||||||||||||||||||
|
��@����`�V�X�e���ƃJ�I�X�V�X�e���͓����ł����H |
1720 |
|||||||||||||||||||||||||||||||||
|
���@����`�n�́C�ɂ߂đ��l�ȐU�����������܂��D�Ⴆ�C�U���\���������ꍇ�C�����ߒ��C�����{����ߒ�(���J�X�P�[�h�ߒ�)�C�t�J�X�P�[�h�ߒ��C�J�I�X�ߒ��ɂ܂ő����̉ߒ����Ƃ蓾�܂��D��ʂɁC�����{����ߒ������ƁC�t�J�X�P�[�h�ߒ������݂��C�]���ăJ�I�X�ߒ��������ƂɂȂ�܂��D���̈Ӗ��ł́C����`�n�̓J�I�X�n�ƌ����Ă��ǂ����ƂɂȂ�܂��D�������C����͒���̌���_�I�J�I�X�ߒ��ɂ��ē����Ă���m���ł���C��ʂ̍������̃J�I�X�n�ɂ��ẮC�ǂ�����������`�������݂��邩�͑S���킩���Ă��܂���D |
||||||||||||||||||||||||||||||||||
|
��@�g�J�I�X(chaos)�h�͂ǂ̂悤�ɒ�`����܂����H |
1730 |
|||||||||||||||||||||||||||||||||
|
���@�g�J�I�X(chaos)�h�̒�`�́C�����҂ɂ���đ����̈Ⴂ������܂��D�����ł́C�ƂĂ�������₷���V���X�^�[(H.G.Schuster)�ɂ���`���Љ�܂��V���X�^�[�̒�`�͈ȉ��̒ʂ�ł��D
�܂��C�x���W�F�C�|���E�C�r�_���́C�p���[�X�y�N�g���ɘA���X�y�N�g�����܂ނ��Ƃ��J�I�X�̒�`�Ƃ��Ă��܂��D���̑������̒�`���Ȃ���Ă��܂��D���̂��Ƃ́C�J�I�X�̖{�����q�ϓI�ɏ\���ɖ��炩�ɂȂ��Ă���킯�ł͂Ȃ����Ƃ���Ă��܂��D
|
�@
�@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ |
|||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||
|
��@�J�I�X�Ƃ͂ǂ������Ӗ��ł����H���ׂƖ�Ă��܂����K�Ȗ�ł��傤���H |
1740 |
|||||||||||||||||||||||||||||||||
|
���@�J�I�X�́C��ʂɁC���ׂƖ�C����I�E�Љ�I�E���_�I�ȍ����C��������ԣ�Ƃ����Ӗ��ɉ�����܂��D�������C�ŋߘb��ƂȂ��Ă���Ӗ��́C���������F��(cosmos)�̏o���̑O�̍���ԣ
�Ƃ�����荪���I�Ӗ��ł�(���̕\1740�Q��)�D���������ڂɂ��鎩�R���ۂ̑����́C���X���X���̎p���C�\���s�\�Ȍ`�ɁC���G�ɕω������܂��D�h��߂����C�킫�オ��_�C���ɗh��߂��̗t���ȂǁC�����グ��ی�������܂���D�J�I�X�����́C�����������G�Ȍ��ۂ̔w��ɒ����������������Ƃ�����̂ł��D���R���ۂɌ��炸���̌��ۂ�Љ�ۂł����Ă��C�����́C���̎��ԓI�E��ԓI�X�P�[���ŁC�K��������(�����\��)�ɂ���C���ꂪ�����̔��q�ɕs���艻���C�ꍇ�ɂ���Ă͍��ׂƂ������(�������\��)��悵�܂��D�������C���܂ł��s����Ȃ܂ܑ��݂������邱�Ƃ͂Ȃ��C�����ꎟ�̈����Ԃɍs�������܂��D����́C�X�����ۂɌ����邠��Ӗ��ł͕��ՓI�Ȏp�ł��D�����C�J�I�X�����Ƃ́C����������ꌩ�����������\�����C���I�E�O�I�v���ɂ���Ē����\�������������������邪�C�Ăю��ȑg�D�I�ɒ����\�����č\������Ƃ������ۉߒ����Ώۂɂ�����̂ł��D�J�I�X�����́C�����C��b�Ȋw���牞�p�Ȋw�Ɏ��邠���镪��œW�J����Ă��܂��D
�@
|
||||||||||||||||||||||||||||||||||
|
��@���n��f�[�^�̃J�I�X���ɂ��āC�g�J�I�X���_�h�ł͂ǂ̂悤�ȕ��@�ʼn�͂��i�߂��܂����H |
1750 |
|||||||||||||||||||||||||||||||||
|
���@���n���͂ɗp������g�J�I�X���_�h�ɂ���āC���n��̃J�I�X���́C���ȑ������C�X�y�N�g����1/f
�����C�A�g���N�^�[�C�|�A���J���E�}�b�v�C���A�v�m�t�w���C���֎������ׂ邱�Ƃɂ���čs���Ă��܂����D�������C�����̕��@�͌��ǂ̂Ƃ���J�I�X���ׂ邱�Ƃɕs�\���Ȃ��̂ł��邱�Ƃ��킩���Ă��܂����D�����̕��@�̑����́C�����̃f�[�^�_����K�v�Ƃ��Ă��āC�Ⴆ�C�l�̐S���ϓ��̑��֎��������߂�ɂ�15�`20�����ɋy�Ԗ��ߍ��ݎ������K�v�Ƃ���C����ɗv����f�[�^�_���͐�10���_�ɋy�т܂��D |
||||||||||||||||||||||||||||||||||
|
��@MemCalc�V�X�e�����J�I�X���n��f�[�^�̉�͂ɗp���邱�Ƃ͂ł��܂����H |
1760 |
|||||||||||||||||||||||||||||||||
|
���@�J�I�X���n��f�[�^�̈����ɑ��āCMemCalc�V�X�e���͋��͂ȉ�͎�i�ƂȂ�܂��D���ɓ��{�����w�����
Journal of the Physical
Society of Japan �ɁC���[�����c�C���X���[�C�_�t�B���O���f���Ȃǂ̃J�I�X���n�f�[�^���ɂ�����炸�Ƃ��Ɏw���X�y�N�g�������������C����т��̎w���X�y�N�g�����������̎��n�J�I�X���n��ł��邩�ۂ��ɂ��Ă̏d�v�Ȓm���ƂȂ�\��������Ă��܂��D���̌����ɂ�MemCalc�V�X�e�����p�����܂����D�܂��CMemCalc�V�X�e����p���čs��ꂽ�J�I�X���n��Ɋւ��錤���ł́C�Ⴆ�J�I�X���n��f�[�^�̃X�y�N�g���ɂ��Ċ�{���[�h�ƍ����g�C���i�K�ɂ킽��T�u�n�[���j�N�X�̏o���C�t�J�X�P�[�h�ߒ��Ȃǂ��m�F����܂��D�����̌�����[���Ƃ��āCMemCalc�V�X�e���̃J�I�X���n��f�[�^��͂ւ̓K�p�����㑝������̂ƍl�����܂��D |
||||||||||||||||||||||||||||||||||
|
��@�����̎��n��f�[�^���炻�̃J�I�X���𒊏o���邱�ƂɊւ��āC����_���f�����Ȃ��C�ΏۃV�X�e���̌���ꂽ���n��f�[�^�݂̂����Ƃɂ��ăJ�I�X�̑��݂��������Ƃ͕s�\�ł��飂Ƃ�������������܂��D���̌����͑Ó��Ȃ��̂ł��傤���H |
1770 |
|||||||||||||||||||||||||||||||||
|
���@���̌����́C��1690,
��1700, ��1710�ŏq�ׂ�����`�V�X�e���̉�͂ɑ��݂���{�����◝�_���f���̏d��ȍ����S���������Ȃ����肩�C�����f�[�^�ɕ�܂���Ă���L���ȓ��e�𗝉��ł��Ă��Ȃ������ł��D���B���C���_���f���̗L�����C���ꂪ��͓I�ɉ�������������`���f���ł����Ă��C���̗L�������d�X�F�߂���̂ł͂���܂����C�����ɂ��̌��E���킫�܂��Ȃ��咣�ɂ��Ă͂����e�F����킯�ɂ͂����܂���D�������C�������Ȃ�ꍇ�ł��C�����f�[�^�C�ϑ��f�[�^�̐�ΓI�Ƃ�������D�ʐ�������܂��D����́C�����f�[�^�C�ϑ��f�[�^������ł��Ȃ����_���f���͔r�������Ƃ���������������炩�ł��D�܂��Ă�C���̂ɂ����鎞�n��̂悤�ȁC���_���f���̒�����������ɂ߂�ꍇ�ɂ́C�Ȃ�����C�����f�[�^�C�ϑ��f�[�^���̂��̂���C�L���ȏ��������ɂ��Ď��o�������d�v�ɂȂ�܂��D�����炱���C�f�[�^���̂��̂ɁC��̐l�דI�ȕt�����������Ȃ��ʼn�͂�����@�̊m�������߂���̂ł����āC���B���C����MemCalc�͂܂��ɂ���ɉ�������̂ł���ƍl���܂��D�@ |
||||||||||||||||||||||||||||||||||
|
��@MemCalc�̓J�I�X���n����ǂ̂悤�Ȋϓ_�Ŏ�舵���Ă���̂ł����H |
1780 |
|||||||||||||||||||||||||||||||||
|
���@MemCalc�́C���n���PSD�ɕϊ����C����PSD�̏���p���Č��̎��n����č\�����邽�߂̈�A�̎葱���ł����C�����ɂ͉���̉�������f�����������������݂܂���D�]���āCMemCalc�ł́C�J�I�X���n������̑��̈�ʂ̎��n����S�������ϓ_�ň����C���ʂƂ��ē�����PSD�̐U��������J�I�X�����o���̂ł��D���X���[�n�ɂ���MemCalc�ɂ���ďڍׂɒ��ׂ�ꂽ���ʂ́CMemCalc�̗D�ꂽ��͔\�͂������܂����D |
||||||||||||||||||||||||||||||||||
|
��@MemCalc�V�X�e���ŃA�g���N�^�[�����߂邱�Ƃ͂ł��܂����H�܂��C�t���N�^�������C���A�v�m�t�w���Ȃǂ͂ǂ��ł����H |
1790 |
|||||||||||||||||||||||||||||||||
|
���@�c�O�Ȃ���C��������V�X�e���ɓ��ڂ���Ă��܂���D�����ŁC������J�I�X�A�g���N�^�[�͖��ߍ��ݎ����Ǝ��Ԓx���ω�������Ɓg�����悤�ɂ��h���̌`��ς��Ă��܂��C���p�I�ł͂Ȃ��Ɣ��f����邩��ł��D�܂��C�t���N�^�������C���A�v�m�t�w�������߂邽�߂ɂ́C�g�J�I�X�Ƃ��Ĉ��̏�ԁh�ɂ��邱�Ƃ����炩���߂킩���Ă���V�X�e������̒���Ȏ��n��f�[�^���K�v�ł��D�V�X�e�������X���X���̏�Ԃ�ω�������ꍇ�ɂ͗��_��C�Ӗ��������܂���D�����ɂ͈��̏�Ԃɂ���V�X�e������̃f�[�^�Ƃ��Ă͔���`�������̉��Ƃ��ċ��܂鐔�l���ȊO�ɑ��݂��܂���D���������Ă�������p�I�ł͂Ȃ��Ɣ��f����邩��ł��D |
||||||||||||||||||||||||||||||||||
|
��@�]���̃J�I�X��͂ɔ�ׂāCMemCalc�V�X�e����p���闘�_�͂���܂����H |
1800 |
|||||||||||||||||||||||||||||||||
|
���@����܂ł̃J�I�X���_�ł́C���X���X�J�I�X�Ƃ��Ă̒��x��ω�������悤�Ȏ��n��f�[�^����͂ł��܂���D�����CMemCalc�V�X�e���͓��ɒZ���f�[�^�̉�͂ɂ����Ă��̂悤�ȕω��𑨂��邱�Ƃ��ł��܂��D
|
||||||||||||||||||||||||||||||||||
|
��@���n��̃J�I�X�����肷�铹��Ƃ��āC�]���C���֎����C�|�A���J���}�b�v�C���A�v�m�t�w���Ȃǂ����p����Ă��܂������C������̏ꍇ���f�[�^�����\���ɒ����Ȃ��Ɩ����Ȍ��ʂ��o�Ȃ��悤�ł��DMemCalc�͒Z�����n��ł̂��̎��g���\�����ڍׂɒ��ׂ���ƕ����܂������C���n��̃J�I�X�����ׂ邱�Ƃ͂ł��܂����D |
1810 |
|||||||||||||||||||||||||||||||||
|
���@���B�́C�Z�����n��(�����̎��n��̈��|�I�����͒Z�����n��ł���)��PSD�Ɋ�Â��āC�J�I�X�����ʓI�Ɏw�������C�ȉ��̂悤�Ȋ���̎ړx�𖾂炩�ɂ��C�_���Ƃ��Ĕ��\���܂���(�Q�l����2-3)�D�����̎ړx�́C���̎��n��f�[�^�̃J�I�X���𖾂����ŋɂ߂ėL���ł��D
|
||||||||||||||||||||||||||||||||||
|
��@��1810�̓��ɂ���@�ɂ��Ď��₵�܂��D ����`���n���PSD�Ƃ��Ă�1/f �X�y�N�g�����ǂ��m���Ă��܂����C�g�w���X�y�N�g���h�Ƃ͂��܂蕷������܂���D����`���n���PSD���w���X�y�N�g���ƂȂ��������Ă��������D |
1820 |
|||||||||||||||||||||||||||||||||
|
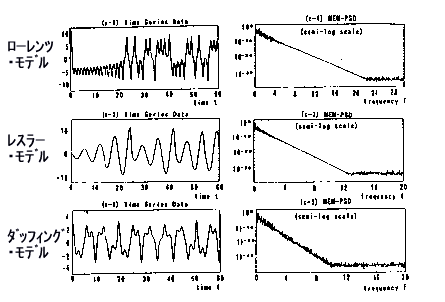
���@�w���X�y�N�g���́C����_�I�J�I�X���܂ޔ���`���ۂɓ��L�Ȑ����ł���C�������ۂȂǂ̎������ʂɂ��Ă��m�F����Ă��܂��D�����̌������\1820�ɂ܂Ƃ߂��Ă��܂��D����C����`���f���ɂ���Đ�������鎞�n���PSD���w���������������Ƃ́C�������̌����ɂ���āC���߂Ė��炩�ɂ���܂����D�}1820�́C�ォ�珇�ɁC���[�����c�C���X���[�C�_�t�B���O�̂R�̌���_�I����`���f���̎��n��f�[�^(��)��PSD�̕Бΐ��ړx(�E)�������܂��D����PSD�̌X���́C�v�Z���x�̌��E�܂Ŏw�������������C������g�w���X�y�N�g���h�ɂȂ��Ă��܂��D����g���̈�́C���n��̍\��(�������C�g�`��f�[�^�̒����Ȃ�)�Ɉˑ��������L�̃X�y�N�g���\���������܂��D�]���āC�w���X�y�N�g���́C�����I�ɁC�����g�������ł��D
�@
|
||||||||||||||||||||||||||||||||||
|
��@��1810�̓��ɂ���A�C�B�C�C�ɂ��Ď��₵�܂��D�����́C��ʓI�ȃJ�I�X�̋��ȏ��ɂ�������Ă��邱�Ƃ��Ǝv���܂����CMemCalc�ɂ���ĉ����V���ɂ킩�����̂ł����H |
1830 |
|||||||||||||||||||||||||||||||||
|
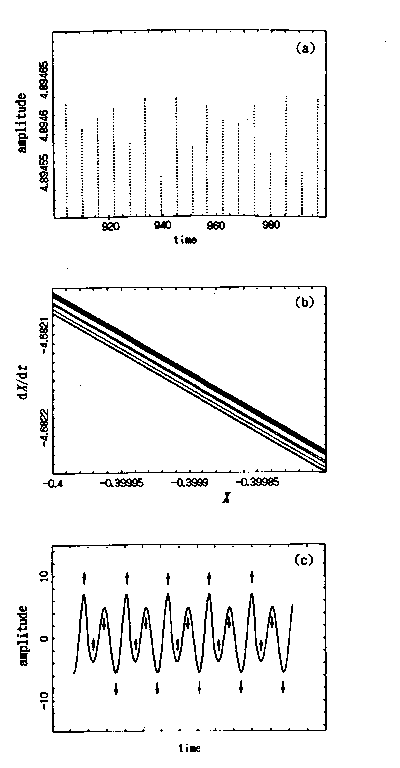
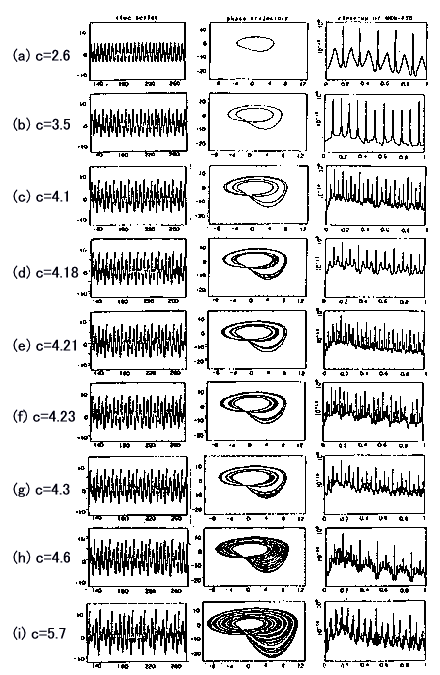
���@�}1830-1(a)�Ƀ��X���[���f���ɂ���Đ������������I���n��̊g��}�������܂��D���}�Ɍ�����悤�ɁC�U���̐U�������ԓI�ɂ�炢�ł��܂��D���̐U����炬�̊T�O�I�Ȑ}�����}(c)�Ɏ�����Ă��܂��D���̐U�����́C�J�I�X�X�y�N�g���ɓ��L�̘A���X�y�N�g���̌���������Ă��܂��D�}1830-2�́C���X���[�E���f���Ɋ܂܂��p�����[�^ c �ɂ��āC���}�͎��n����C���}�̓g���W�F�N�g���[���C�E�}��PSD�̒���g���̈�̊g��}�������Ă��܂��D����́C�ォ�珇�ɁC�p�����[�^c = 2.6�ɂ����������Ԃ���C�p�����[�^c = 3.5����c = 4.23�̎����{���ߒ����o�āC�����ăp�����[�^c = 4.3����c = 5.7�̋t�J�X�P�[�h�ߒ��܂ł̌��ʂ������Ă��܂��D�S�Ă̌��ʂŁC�X�y�N�g���s�[�N�̈ʒu�Ȃǂ��C���_�l�������ɍČ����Ă��܂��D�����Œ��ڂ��ׂ��Ȃ̂́C(a)c = 2.6�̌���(�ŏ�i�E�})�Ɍ����镝�̍L���s�[�N�ł��D���̕��̍L���s�[�N�́C�n�̔���`�s���萫�ɂ���Đ������ꂽ�C���n��̐U����炬����R������ƍl����܂��D�����̕��̍L���s�[�N�́C(b)c = 3.5��(c)c = 4.1�Ŋϑ������悤�ɁC�J�I�X��Ԃŗǂ��m���Ă�������{���ߒ��̎��̏�ԂŐ������C�����Ĉ��艻����܂��D�����Ă����̕���s�[�N�́C(g)c = 4.3, (h)c = 4.6������(i)c = 5.7�Ŋϑ������悤�ɋt�J�X�P�[�h�ߒ��ŏ��ł��܂��D�@�ȏ�̂悤�ɁC���X���[�E���f���̂悤�Ȍ���_�I����`�͊w�n�ł́C�n�̔���`���ɋN������s���萫�ɂ��U����炬�������C���̂�炬�̎��g���́C���镽�ϒl�̎���ɕ��U���C���ꂪPSD�̘A���������\�����܂��D��炬�́Cc �̂���l�ň��艻���C���ώ��g���݂̂����U���̎����I�ȐU���ƂȂ�C���ꂪ�s���������a�g�B�����܂��D�܂�C�����{����ߒ��ł́C���̍L���A���������\��������܂��D�����āC�t�J�X�P�[�h�ߒ��ł́C�������a�g�̃s�[�N���z������܂��D�����C�J�I�X�I����(chaotic mixing)�ɂ����g���ϒ��ɂ����ł��N����ƂƂ��ɁC�����I�ɋK�������č\�����܂��D�t�J�X�P�[�h�ߒ��Ƃ́C�������������{����ߒ��ō\�������ꂽ�A���̈悪�č\�������ߒ��ƂƂ炦�邱�Ƃ��ł��܂��D
|
||||||||||||||||||||||||||||||||||