|
|
§4 実データのMemCalcによる解析
|
|
§§4-3 非線形・カオス時系列(その2)
|
|
|
|
|
問 現実の生体時系列データについて得られた3Dスペクトルアレイから,生体現象(機序)に対する重要な知見が得られた例はありますか?
|
1840
|
|
|
|
|
答 図1840に,健常者の血圧脈圧波の時系列(上段
case1)が,自律神経障害者の時系列(下段
case2)と比較して示してあります.ここでは,上段の健常者の結果について注目します.
中央に示されている3Dスペクトルアレイにおいて,基本モードとその高調波が明瞭に観測されますが,ここでの特徴は以下の2つにあります:①基本モードのパワーが圧倒的割合を占める,および②高調波のゆらぎが高次になるにつれて大きくなる.
前者は,ヒト(生物)が生きるためには,エネルギーを常に外界から取り込んで全身に送り続けることが必要であり,その役割を心臓が果たしているという事実を意味しています.言い換えるならば,これは一般にあるシステムが非線形現象を示す場合,そのシステムは常にエネルギー補給がされていなければならない(これを開放系と呼ぶ)ということに相当しています.後者は,心臓の拍動が内因的・外因的影響に柔軟に応答している事実を示しており,いわゆる“微調整”応答としての“ホメオスタシス”的制御の結果を意味しています.こうしてヒト(生物)は,高調波モードの“微調整”応答を伴った基本モードの支配的パワーによるエネルギー的安定性によって,生物としての“ホメオスタシス”を実現していると解釈されます.
“ホメオスタシス”という概念は,とかく“微調整”機能の側面から論じられていますが,むしろ“エネルギー的安定性”のほうが本質的に重要であって,この事実を初めて物理量として認識できたものと言えます.下段の自律神経障害者の場合は,この“微調整”機能が損なわれていますが,当然のこととして,生きるためのエネルギー補給は維持されていなければならないから,この事実はやはり基本モードの卓越として3Dスペクトルアレイの振舞いに示されています.
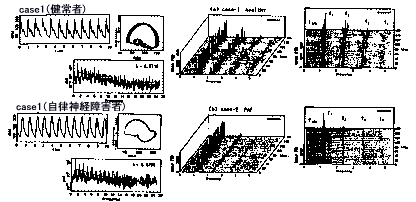
図1840 健常者(case-1)と自律神経障害者(case-2)に対する,波形として測定された時系列データ,d(data)/dt-data平面上の位相トラジェクトリー,MEM-PSDの片対数プロットおよび3Dスペクトルアレイ.
|
|
|
|
|
|
問 指数 PSDの傾きの値は何を意味しますか? |
1850
|
|
|
|
答 指数スペクトルの傾きが意味する内容は重要です.今,決定論的力学系を考えると,その系には,一般に,決定論的力と揺動力(確率的力)が作用しています.実際の物理系の振る舞いは,どちらの力が支配的かに依存しています.例えば,確率的力が支配的な場合,系の振る舞いは指数スペクトルを作りません.指数スペクトルは,系が決定論的力が支配的である場合に生じます.レスラー,ローレンツ,ダフイング系はこの場合に属します.
図1850にレスラーモデルに含まれるパラメータc の値に対して得られる時系列から計算されたMEM-PSDの指数スペクトルの傾きの変化を示します.同図に見られるように,指数スペクトルの傾きλは,周期状態から分岐過程を経由するに従い減少し,カオス状態で最小になります.一般に,決定論的力学系から生成される周期的非線形波動では,ゆらぎの影響が小さければ,λの値は大きくなります.即ち,高周波数成分が速やかに減衰します.一方,非線形系では,ゆらぎの影響が全く新しい形で入ってきます.即ち,系の非線形性による不安定性に起因する振幅ゆらぎ(amplitude fluctuation)の存在であり,これの成長に伴い,指数スペクトルの傾きが小さくなります.即ち,高周波数成分が速やかに減衰しなくなります.
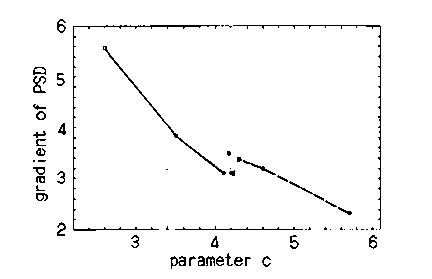
図1850 パラメータc
に対するMEM-PSDの傾き.
実線:分数調和波分岐,破線:逆カスケード.
|
|
|
|
|
問 指数スペクトルの傾きは,時系列の長さや時間領域によって変化しませんか?
|
1860
|
|
|
|
|
答 ここでは,ロ-レンツ・モデルに対する短い時系列に対するPSDの計算結果を示します.図1860-1(b-1)~(b-5)は,それぞれ,同図(a-1)~(a-5)の2000点,1000点,500点,250点および125点のデ-タ(それぞれ,40.01~60.00,40.01~50.00,40.01~45.00,40.01~42.50および40.01~41.25の時間領域に対応している)に対するMEM-PSDの片対数プロットを示しています.全体のスペクトルの減衰もまた,それらが約
f
=18~20で平らになるまで指数的です.ロ-レンツ・モデルの短い時系列の場合における
λ の平均値が,表1860-1に,ダフィング・モデルのものと一緒に,リストされています.括弧の中の値は
λ の値の範囲を示します.λ
の値のバラツキは2つのモデルでは比較的小さいことがわかります.
指数特性は,デ-タの時間領域に関係無く,カオス時系列の任意のセグメントにおいて,普遍的に見られます.例えば,ロ-レンツ・モデルの場合,30.01~35.00の間の時間領域における500点のデ-タ(図1860-2(a-1))に対するMEM-PSDの片対数プロットと50.01~52.50の間の時間領域における250点のデ-タ(同図(a-2))に対するものとが,それぞれ,同図(b-1)(λ=3.99)および(b-2)(λ=4.12)に示されています.短い時系列に対するλの値は,125点デ-タに対する値を除き,長い時系列(デ-タ長6000)に対するものより幾分大きくなっています.これらの特徴はダフィング・モデルに対しても当てはまります.
指数特性は,また,レスラ-・モデルの場合にも認められます.しかしながら,状況は,上述したこれら2つの場合とはかなり違っています.レスラ-・モデルの種々のセグメント時系列に対するλの値が表1860-2にリストされています.表に見られるように,λの値の強い波形依存性が明瞭に見られます.
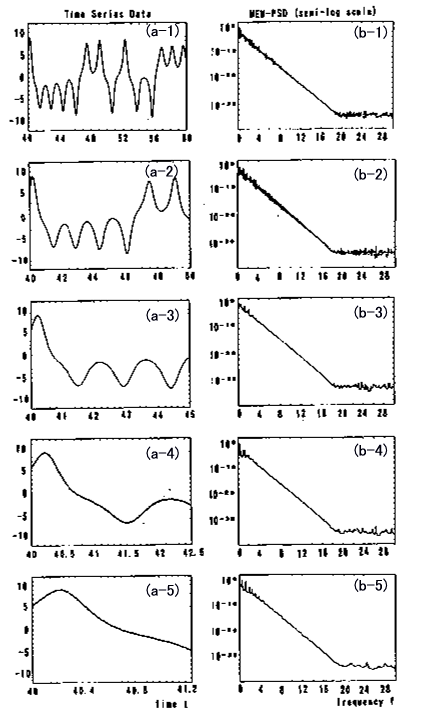
図1860-1 ローレンツ・モデルの短い時系列(左)に対するMEM-PSD(片対数スケール)(右).
(a-1)と(b-1)データ長2000について,(a-2)と(b-2)データ長1000について,(a-3)と(b-3)データ長500について,(a-4)と(b-4)データ長250について,(a-5)と(b-5)データ長125について.
表1860-1 ローレンツとダッフィング・モデルの場合の
セグメント時系列データに対するλの平均値
| Data length |
Lorenz model
(range) |
Duffing model
(range) |
| 2,000 |
3.65
(3.35-3.90) |
7.36
(7.28-7.46) |
| 1,000 |
4.06
(3.24-4.98) |
7.49
(7.30-7.91) |
| 500 |
4.32
(3.23-5.59) |
7.52
(7.15-8.35) |
| 250 |
4.49
(3.19-6.18) |
7.75*
(6.69-8.86) |
| 125 |
4.44
(3.22-5.86) |
7.06*
(5.23-8.25) |
*The
averaged values except the outliers.
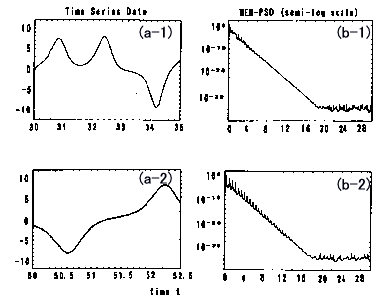
図1860-2 ローレンツ・モデルの短い時系列(左)に対するMEM-PSD(片対数スケール)(右).
(a-1)と(b-1)時間領域30.01~35.00における500点データについて,
(a-2)と(b-2)時間領域30.01~35.00における250点データについて.
表1860-2 レスラー・モデルの場合のλ値の波形依存性.

|
|