←　前節(§§３−３)へ

問　ある種の時系列データを解析する目的の一つは，将来におけるその挙動を予測することにあります。しかし、そもそも予測とは常に可能なものなのでしょうか？

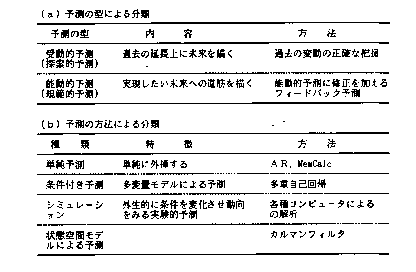
答　予測には，受動的予測と能動的予測の２通りがあります．受動的予測は，過去から現在までの推移から未来を推し計るものです．一方，能動的予測とは，受動的予測を基礎としつつも，未来における期待値をあらかじめ設定し，それに向かうように現象を推移させようとするものです．しかしながら，この能動的予測の場合，現象の客観的推移を正しく把握することが前提になるため，受動的予測の側面をいいかげんにすることは許されません．こうして，予測というのは，結局は過去から現在までの現象の推移をどれだけ正確にとらえきれるかという問題に帰着することになります．その上で，未来に起こる現象の要因は無数にあり，その全てを私たちがあらかじめ知ることは不可能ですので，予測には常に限界がつきまといます．

問　これまでの予測解析の考え方は，どのようなものですか？

答　これまでの予測解析の考え方は，過去の時系列に含まれる誤差と未来における未知部分とが存在することを理由に，確率的・統計的予測が大勢を占めてきました．しかしこれでは結局，予測を非決定論的世界に落とし込むことになってしまいます．一方，経済分野(特に，大手証券会社や銀行)で構築されている“意思決定支援システム(MSS：management support system)”における環境予測システムでは，30〜50本の構造方程式，同数程度の定義式，100を優に超える内生変数と外生変数などからなる多元連立非線形方程式群を大型コンピュ−タで解いて解を求めます．これは決定論的ではありますが，非線形方程式の困難さを度外視した方法で全く意味をもちません．こうした状況の結果として予測の科学性，客観性が失われ，｢予測は当たらない｣とか｢予測は困難である｣などと言う評判が流布し，“賭け・卦・占い”の類と同一視されることになっています．

問　近年，非線形時系列の予測解析の研究が盛んに行われていますが，あまりうまくいっているように見えません．この原因は何だと思いますか？　

答　カオス時系列の予測に関しては，代表的な研究の成果がA.S.WeigendとN.A.Gershenfeld編 "Time Series Prediction -Forcasting the Future and Understanding the Past-"(1994)にまとめられています．その教科書では，カオス時系列の予測法として，自己回帰(AR)法，時間遅れの埋め込みによる状態空間の再構成そしてニュ−ラルネットワ−クなどのいくつかの注目すべき方法が紹介されています．この中でARはカオス過程には不適当です．なぜなら，AR過程に基づく線形モデルは，カオスのような非線形系を記述することは不可能であると考えられるからです．他の２つの方法は，予測の手続きをマスタ−することが簡単ではありません．

問　MemCalcでは，予測解析は可能ですか？　

答　予測の基本は，過去から現在までの変動構造を調べ，それを未来に延長して未来の変動構造を推し量ることです．MemCalcを用いることによって，この基本に立ち戻り，改めて科学的・客観的な予測の方式を確立できます．表1230に，予測の種類がまとめられています．このまとめからも分かるように，予測の基本としては，何よりも先ず“過去の時系列の構造の正確な解明”が大前提になります．MemCalcは，所与の時系列の変動構造，とりわけ周期構造，を解明する点では，圧倒的に優秀な解析システムです． 
　MemCalcを予測解析に用いる試みは，これまでに様々な時系列に関して行われました．中でも，一連のカオス時系列に対する理論的観点からのアプロ−チや，幾つかの実際の時系列デ−タ，例えば，太陽黒点数デ−タ，感染症発生数デ−タ，そして各種の経済時系列デ−タなど，に対する実用的観点からの予測解析が行われました．その結果，MemCalcが予測に十分活用できることが実証できただけでなく，従来の予測に対する考え方自体にも一定の修正が必要であることが明らかになりました．

表1230 予測の種類．

問　MemCalcでは予測解析はどのように行いますか？

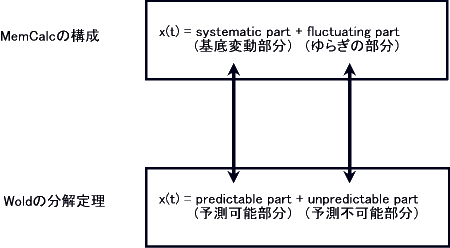
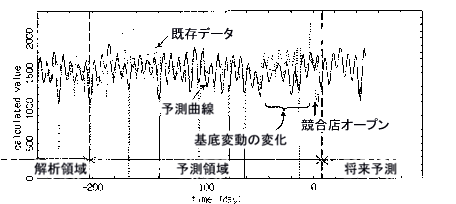
答　MemCalcでは，その比類なき卓越した“時系列変動構造の解析能力”を利用して，過去の時系列の変動構造を決定し，それを未来に延長します．過去の時系列の変動構造は，MemCalcの構成要素として導入した“基底変動”として求められます．MemCalcによって決定される“基底変動”は，ウオルドの分解定理(Wold's decomposition theorem)における“予測可能部分(predictable part)”に数学的表現形式も含め対応しています(図1240)．こうして，MemCalcによる予測は，過去の時系列の構造を完全に把握し，それを未来に延長する結果，過去の構造がどこまで持続するかの検討が可能となります．即ち，過去の状況と違った未来の新たな状況をはじめてとらえることを可能にしています．
　過去の構造が未来のどの時点まで持続するかの検討は，過去の既知のデ−タ領域に，解析区間と予測区間を設定し，解析区間の時系列の“ 基底変動”を完全に表現する数学関数表現を得て，その表現を予測領域において再計算し，既存のデ−タ値と比較することによって可能となります．このことによって，はじめて予測の精度や信頼性の評価も可能となります．この手続きは，高精度の周期構造抽出能力と最小二乗あてはめ能力とが結合したMemCalcによって可能となったものです．私たちの予測の手続きは，太陽黒点数の変動の場合のような比較的強い周期性を持つ時系列の予測に実に有用であり，カオスの場合についてもまた満足すべきものとなっています．

図1240　MemCalcの基本となる考え方とウオルドの分解定理．

問　MemCalcによる予測解析が他の方法よりも優れていることを示す具体的な事例はありますか？

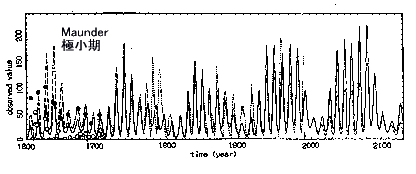
答　太陽黒点数は，多くの研究者によって時系列解析方法のテスト用のデ−タとしても用いられてきましたが，太陽黒点数の変動を説明できる解析方法はこれまで皆無であり，まして“小氷河期”に関わっている“マウンダ−極小期”も含めてとなると，全く絶望的でありました．説明できないことの理由に，太陽活動は不規則で予測不能な振舞いをする(最近ではカオス変動と言われている)，あるいは太陽黒点数が ウｵルフ(Wolf)による評価方法によって算出されるため，かなりあいまいな量となっている，などが指摘されていました． 
　確かに太陽黒点数にはかなりあいまいな部分があるので，私たちも，MemCalcによって，その“基底変動”を決定するには注意が必要であったのは事実です．しかし最終的に，1700〜1992年の292年間の“基底変動”はわずか５つの周期モ−ドで十分説明できることが判りました．そこで，1700〜1992年間を解析区間として予測解析を行ったのです．その結果，図1250-1の実線に示されているように，1600〜1700年間の太陽黒点数の変動が，ショ−ヴの評価(黒丸)に一致すること，マウンダ−極小期は，太陽活動の規則的変動の範疇で説明できること，そしてまた，その時期のデ−タとしてはショ−ヴのデ−タの方が客観性をもつと考えられることが明らかになりました．
　更にまた，過去2000年間と未来1000年間の予測(図1250-2(a))の結果は，平均太陽黒点数の状況(図1250-2(b))に示されるように，過去にあったとされる４つの“小氷河期”(図1250-2(c)に示されるオ−ルト(Oort)，ウオルフ(Wolf)，シュペ−ラ(Sporer)そしてマウンダ−の４極小期)に相当する極小期を見事に再現しています．
　以上の成果は，ひとえにMemCalcの高い時系列構造分析能力とその解析の方法論的優秀性を示すものです．こうして，太陽は，マウンダ−極小期の“異常な”振舞いを含めて，規則的で予測可能な星であることが判明したのです．そして，太陽活動は不規則で予測不能な振舞いを示すとか，太陽黒点数にあいまいさがあるなどの理由のために，従来の解析方法では解析できなかったのではなく，むしろ従来の解析方法の限界によるものであったと考えられます．

図1250-1　太陽黒点数の予測解析．
●：Schoveの評価，○：Eddyの評価．予測曲線：実線．解析区間：1700〜1992．1600〜1700年間(マウンダー極小期)の太陽黒点数の変動はショーブの評価(●)に一致する．

　

図1250-2　3000年にわたるシュミレーション．(a)太陽黒点数の変動，(b)各々の100年毎の極小期のサイクルにわたって平均された太陽黒点数，(c)年輪年代学から評価された太陽活動の水準．

問　これまでの経済データの予測解析はことごとく失敗しているようですが，MemCalcではどうですか？

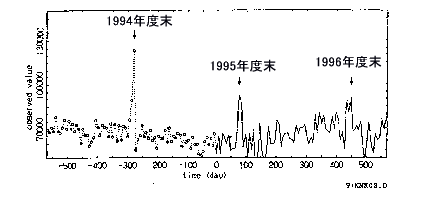
答　MemCalcを用いた経済デ−タ変動の予測解析は，数年前から，ユ−コ−プ事業連合(神奈川生協を中心とする事業連合体)において実施されてきました．現在莫大な種類と量の時系列デ−タの解析を通して，経済データに対するMemCalcの活用の可能性の実証をほぼ終了しています．　
　図1260-1には，生協のある店舗の来店客数の毎日の変動データ(点線)と予測曲線(実線)とが示してあります．予測曲線が，予測区間において，実績データをかなり忠実に再現していることが了解されます． 
　更に興味深い結果を図1260-2に示します．これは，神奈川生協の小型店週間供給高の82週(約１年半)にわたる時系列デ−タです．この時系列には，ほぼ50週目辺りに年末期の供給高の大幅な増大が見られます．これを解析して求められた予測曲線は，実績との比較で誤差は数％(10 ％以内)であり，ほぼ予測としては成功しています．この成功以上に注目すべきは，年末期の利用客数の増大が，過去の時系列中に１度しかなく周期的になっていないにもかかわらず，次の年末期について，正しい時期に供給高の増大が見事に再現されたことです．この結果は驚くべきものであって，従来の時系列解析の常識では理解できないものです．MemCalcはどうしてこうしたピ−クを再現できたのでしょうか．それは次のように考えることができます．
　利用客数の変動の周期構造は実に複雑で，MemCalcによればほぼ28種類のリズムの存在が確認されています．この多重リズムが，振幅と位相を揃えて年末のピ−クを再現しているのです．このことを別の言い方をすれば，年末のピ−クは年間を通した変動の集約的表現にもなっているということです．｢時系列における任意時刻の値は，それ以前の時刻の値に何等かの影響を受けており，また，未来の値は過去から現在までの推移に何等かの影響を受けている｣ということを問0020で指摘しましたが，この結果は正にそうした時系列の本質的性格を見事に目に見える形で示しています．この事例も，MemCalcが，時系列の変動の周期構造をいかに正しくとらえているかということを如実に示している好例です．

図1260-1　MemCalcによる予測解析の事例−生協店舗の来店客数−

　

図1260-2　神奈川生協の小型店週間供給高時系列データとその予測．

問　MemCalcは短い時系列の解析にも有用であるということですが，それは予測解析にも言えますか？

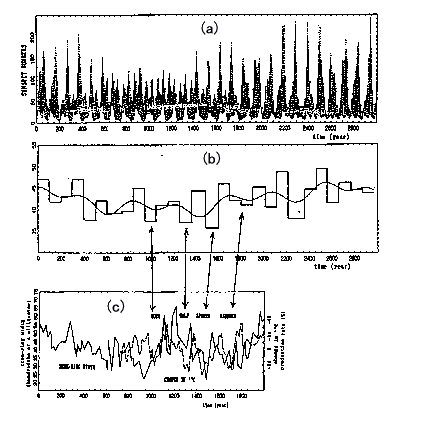
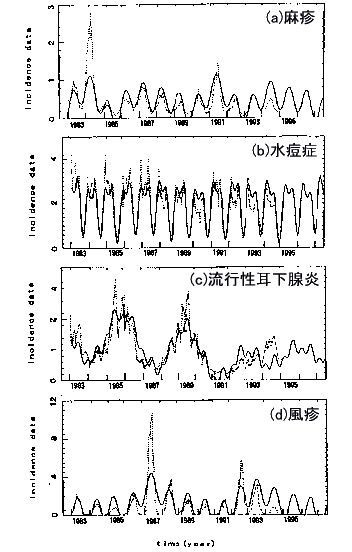
答　MemCalcによる短い時系列の予測解析の例として，感染症サーベイランスにおいて蓄積された，データ長500点の感染症発生患者数の結果があります(参考文献2-6)．図1270に，(a)麻疹，(b)水痘症，(c)流行性耳下腺炎(ムンプス)，(d)風疹についての結果を示します．図1270では，解析領域(1983〜1992)のLSF曲線(実線)が原データ(点線)の基底変動を十分に再現していることが見て取れます．予測曲線は，このLSF曲線を解析領域(1983〜1992)から予測領域(1993〜1994)に延長することによって得られます．各感染症の予測解析の結果は以下のとおりです．

図1270　最適LSF曲線の原データとの比較．(a)麻疹，(b)水痘症，(c)流行性耳下腺炎(ムンプス)そして(d)風疹．実線：解析領域の最適LSF曲線と予測領域でのその延長線，点線：解析領 域の原データ(1983〜1992)，破線： 予測領域 の原データ(1993〜1994)．

問　予測の程度(正確さ)をどのような基準で評価するのですか？

答　MemCalcを用いた予測解析の主要な目的は，あてはめ度の高いLSF曲線を計算するのではなくて，原データの基底変動を構成する主要な周期モードを決定して，これらの周期モードを予測解析に用いることにあります．
　あてはめ度を評価する方法の一つとしては，LSF曲線と原データの差の標準偏差を求めることです．この残差データの標準偏差は，スペクトル解析の結果から得られたパワー値の大きい周期モードを一つずつLSF曲線にとりこむにつれて，大きく減少していきますが，あるモード数を越えると，その減少の度合いが小さくなります．このことは，解析対象の時系列データ長の範囲で周期構造が除かれることが，標準偏差値の大きな減少に寄与し，ゆらぎ成分は標準偏差を低下させないこと，即ち，標準偏差が大きく減少し続ける周期モードが原データの基底変動を構成し，それ以外の周期モードが原データのゆらぎを構成していることを意味します．
　LSF曲線に取り入れる周期モードの数を増やすほど，標準偏差の値は小さく，すなわちあてはめ度はより高くなりますが，このゆらぎの部分の周期構造は時々刻々と変化するので，予測曲線を得ることを目的として計算するあてはめ曲線にゆらぎの部分の周期構造を取り入れても意味がありません．

↑ページの先頭へ

←　前節(§§３−３)へ