|
���P�@���n���͈�� |
|||||||||||||||||||||
| �����P�|�P�@���n��(���̂Q) |
|||||||||||||||||||||
| �@ | |||||||||||||||||||||
|
��@���n��̑��d�\���Ƃ����\����ڂɂ��܂������C����͂ǂ̂悤�Ȃ��̂ł����H |
0090 |
||||||||||||||||||||
|
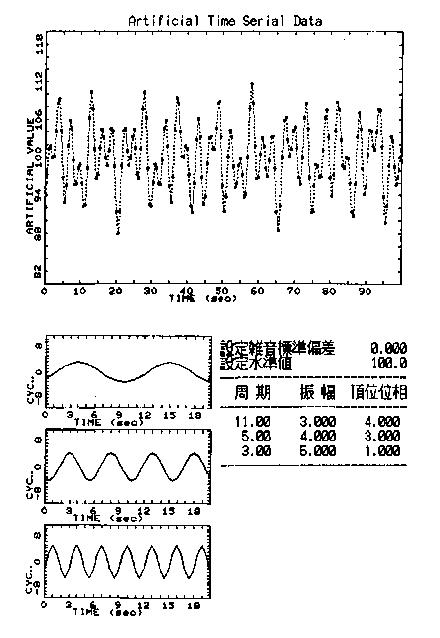
���@�}0090�̏�i�Ɏ������n��́C�ꌩ�s�K���ȃ����_���ϓ��ł��邩�̂悤�Ɍ����܂��D�Ƃ��낪���͂��̎��n��́C�킸���R�ʂ�̎��������ŕ`�����g(�}0090���i)���C�ʑ��ƐU�����Ⴆ�ďd�ˍ��킹�邱�Ƃɂ���č��o���ꂽ���̂ł���C�����_���ϓ��ł͂���܂���D���̂悤�ɕs�K�����n��͕K������(����)�̎����̔g�̏d�ˍ��킹�ɂȂ��Ă���ƍl�����܂��D����͎��n��̑��d�\�����������ł��ȒP�ȗ�ł��D��蕡�G�ȗ�Ƃ��ẮC��0070�Ɏ������t���N�^���\�����������n����܂��D
|
|||||||||||||||||||||
|
��@�ǂ̂悤�ɂ����玞�n��̑��d�\�����L�q�ł��܂����H |
0100 |
||||||||||||||||||||
|
���@���n��̑��d�\���Ƃ́C���n��X�̔g�̏d��ł����č\���������ϓ��ƁC����ɕt��������炬�̕����Ƃ̂Q�̕������琬�邱�Ƃ������܂��D�����Ŏ������́CMemCalc�̉�͗��_�̍\���v�f�Ƃ��āC�����Œ�`�����g���ϓ� underlying variation�h�Ƃ����T�O�����Ă��܂��D
�����ŁCX
( t
)�͔C�ӂ̎��n��CXUV
( t )�͂��̎��n��̊��ϓ��C��( t
)�͂�炬�̕����ł��D��炬�̕����́C��_�I�ȁg�����_���G���h�ł���ꍇ�ƁC����_�I�ȃ_�C�i�~�N�X�Ɋ�Â����̂ł���ꍇ������܂��D���̊��ϓ��́C�T���v�����O���ԊԊu�����傫�ȕϓ������C�����C�g�L�ӂȕϓ��h�̂��Ƃ��Ӗ����Ă��܂��D���n���͂ł́C���́g���ϓ��h�����肷�邱�Ƃ����S���ł��D
|
|||||||||||||||||||||
|
��@���n��f�[�^�̑��d�\���́C���̃f�[�^�𑗏o�����V�X�e���̐ÓI�\���C�܂��͓��I�\���Ƃǂ̂悤�ɑΉ�����ƍl�����܂����H |
0110 |
||||||||||||||||||||
|
���@�V�X�e���̍\���v�f�̉^��(���I�\��)�Ƌ�ԓI���z(�ÓI�\��)�Ƃ͖��ڂɊW���Ă��܂��D�Ⴆ�C��ԓI���z���K���I�ȏꍇ(�����\���͂��̓T�^)�C�V�X�e���v�f�̉^���͂��̋K�����̎x�z���C�ŗL�̉^�����[�h(�ŗL�U��)���Ƃ�܂��D�ŗL�^��(�ŗL�U��)���[�h�̓X�y�N�g���Ƃ��Ċϑ�����C�K��������̂���̓X�y�N�g�����̍L����Ƃ��Č���܂��D
|
|||||||||||||||||||||
|
��@���n��̑��d�\���͎��g�����(�X�y�N�g����)���������I�ȋ���������܂����H |
0120 |
||||||||||||||||||||
|
���@���n��̑��d�\���́C��0100�ŏq�ׂ��悤�ɁC����_�I����(���ϓ�)�Ƃ�炬�̕������琬���Ă���ƍl�����܂��D���n��̊��ϓ����\����������\���́C�X�y�N�g����ł́C����g���̈�̎x�z�I�ȃX�y�N�g�����Ƃ��̍����g�Ƃ��Č���܂��D���n��̂�炬�̕����́C�X�y�N�g�����̕��̍L����Ƃ��āC���邢�͕��̍L���A���X�y�N�g���Ƃ��Č���܂��D |
|||||||||||||||||||||
|
��@���n��́g���ϓ��h�Ƃ͋�̓I�ɂǂ̂悤�Ȃ��̂ł����H |
0130 |
||||||||||||||||||||
|
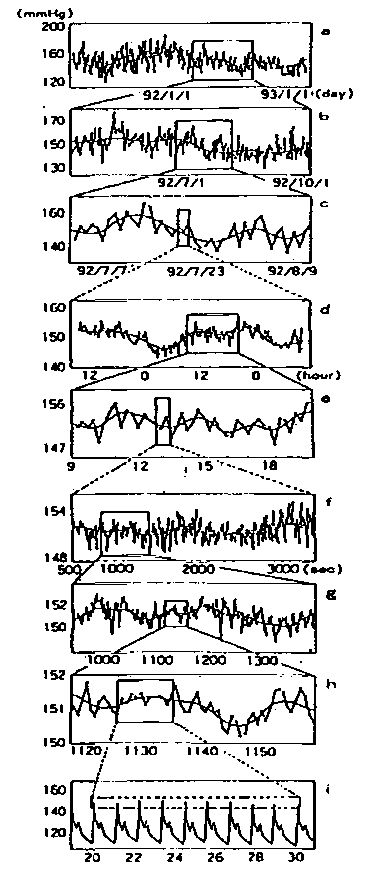
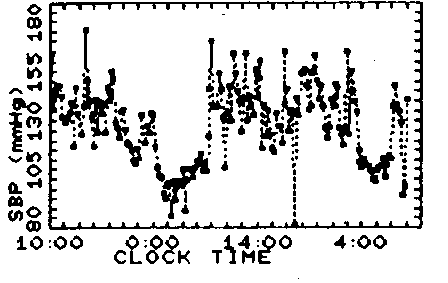
���@�Ⴆ�C24���Ԍ����f�[�^(ABPM�f�[�^)�ɂ����ē������Y�������߂邱�Ƃ́C���̎��n��̊��ϓ������߂邱�Ƃ��Ӗ����܂��D�}0130�ɃT���v�����O�Ԋu�̈قȂ錌���̎��n��f�[�^�C�����ĕ\0130�ɂ��̑�������������܂��D�e���ԃX�P�[���̎��n��ɂ��Ă͂߂ĕ`���ꂽ�Ȑ����g���ϓ��h�������Ă��܂��D�����Ă��́g���ϓ��h���̂��C�傫�Ȏ��ԃX�P�[���̎��n��̎��ԗ̈�ɉ����ėl�X�ɕω����܂�.
|
|||||||||||||||||||||
|
��@���n��f�[�^�̒���(���ϑ�����)���������������ď������ϓ���Ƃ��C�ǂ̂悤�Ȍ��ʂ����҂���܂����H |
0140 |
||||||||||||||||||||
|
���@���n��f�[�^�̒���������ɂ�āC��蒷�����̃��[�h�����n��f�[�^�̊��ϓ����\������������[�h�Ƃ��ĕ]�������\��������܂��D���̒��������[�h�̌��Ƃ��ẮC���̎��n��̇@�������̎����ϓ��ƇA�X���ϓ��̂Q�̏ꍇ���l�����܂��D
�@
|
|||||||||||||||||||||
|
��@���̃f�[�^�ɂ���o�σf�[�^�ɂ���C�f�[�^�����ǂ̂悤�ɂƂ��Ă����̒����Ɂg�K�������h���ϓ��������������悤�ł����C���̎����͉����Ӗ����܂����H |
0150 |
||||||||||||||||||||
|
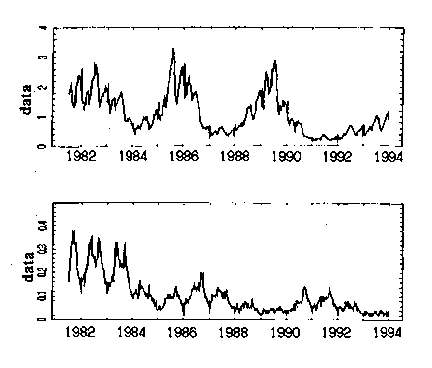
���@�Ⴆ�C24���Ԍ����f�[�^(ABPM�f�[�^)���������đ��肵�C48���ԃf�[�^���Ƃ��C�����̏ꍇ�C48���ԃf�[�^�ɓ������Y��(24���Ԏ���)�͕��ՓI�Ɍ���������܂��D���]�̔������f�[�^��o�σf�[�^�ł́C365��(�P�N)�������f�[�^���Ɋւ�炸����������܂��D����͎��n��f�[�^�ݏo�������ۂ̔w��ɑ��݂���n�������Ă���ŗL�ϓ��̎����ł��D���n���̖͂ړI�́C���������ŗL�ϓ������ϓ��Ƃ��ċ��߂邱�Ƃɂ���܂��D |
|||||||||||||||||||||
|
��@�g��炬�h�Ƃ����w�p�p��͂��܂��܂ȋǖʂŎ��ɂ���悤�Ɏv���܂��D�ǂ̂悤�ȏꍇ�ɂǂ̂悤�ȈӖ��Ŏg����̂��C���n��Ƃ̂Ȃ���̐[����������Ă��������D |
0160 |
||||||||||||||||||||
|
���D�w�p�p��Ƃ��Ắg��炬fluctuation�h�́C���v�����w�ɂ����邻�̈Ӗ��𗝉����邱�Ƃ��d�v�ł��D���v�����w�ɂ�����g��炬�h�́C���X���X�ϓ����錻�ۂɊւ��邠������̌��Ƃ��čl�����Ă��܂��D���̉��߂ɗ��ĂC�g��炬�h�͋ɂ߂čL�͈͂̓��e�������C����Ӗ��ł͂����܂��ɂȂ炴����C�]���āC���v�����w�ł͐��w�I���_��O��Ɂg��炬�h��莮�����Ĉ����܂��D |
|||||||||||||||||||||
|
��@�Ȃ��C���n��f�[�^�́g�{���I�Ɂh����`�����܂�ł���̂ł����H |
0170 |
||||||||||||||||||||
|
���@���n��f�[�^�̒l���C���鎞�ԓ_���玟�̎��ԓ_�֕ω�����ꍇ�C�n�͗l�X�ȑ��ݍ�p���܂��D���n��ݏo���n�́C�Ǘ��n�ł͂Ȃ��C���͂Ƃ̊Ԃʼn��炩�̉e�����y�ڂ������Ă��鑊�ݍ�p�n�ł��D���̑��ݍ�p�̎��ԓI���ڂ́C�n�����͂ɉe����^���C���̉e���������͂̌n���Ăь��̌n�ɉe����^���C���̉e�������n���X�ɂ܂����͂ɉe������Ƃ����悤�ɁC����Ώیn�Ǝ��͂̌n�Ƃ̊Ԃ̑��ݍ�p�͖����̘A���ƂȂ�C�������������̘A���̑��ݍ�p�́C��ʂɔ���`�ƂȂ�܂��D �@ |