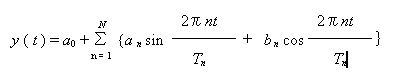|
§1 時系列解析一般
|
|
| §§1−2 時系列解析 |
|
|
問 時系列解析方法の種類と特徴を簡単に説明してください. |
0180 |
|
答 時系列解析法は2種類の解析から成ります.一つは周波数領域における解析,もう一つは時間領域における解析です. |
|
|
問 時系列データを解析するとは具体的にどのような事柄を意味するのでしょうか? |
0190 |
|
答 観測される時系列データx(t)は,問0100で述べたように,決定論的部分(基底変動)とこれに付加されるゆらぎの部分との2つの部分に分けて考えることができます.時系列データの解析は,この2つの部分をどう定量的に評価するか,ということです. |
|
|
問 定常性の検証が必要と言われますが,これは可能ですか? |
0200 |
|
答 多くの時系列解析理論は,定常性を前提にして構成されています.定常性とは,時刻−∞〜+∞で観測される無限長時系列について,平均値一定,分散が有限な場合を意味します.定常性とは理論構成上,−∞〜+∞の時間領域において定義される概念です.これまでの時系列解析の理論は,−∞〜+∞の長さの時系列を対象として来た結果,実際の解析対象時系列への理論の適用にあたって,その時系列が定常性をもつことが必要とされてきました.しかし,現実のデータは有限であり,定常性の定義に従って厳密に検証することは不可能で,最終的には“定常と見なす”ということになります.又,多くの現実の時系列は,漸増(漸減)するパターンであったりし,定常性は明らかに認められない,“定常と見なす”ことができないものがあります.従って,こうした定常性を解析の前提にすることは,現実の時系列解析では得るところは少なく,むしろ避けるべきです. |
|
|
問 「非線形に加えて非平衡,非定常,ゆらぎの性質に無関係に解析する」とはどのようなことですか? |
0210 |
|
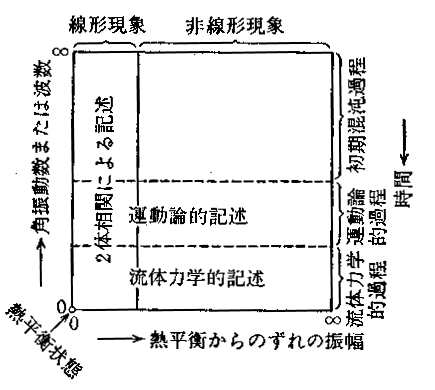
答 一般に現象は何らかの初期的変動(初期混沌過程)から次第に系全体が平衡化し,最終的には熱平衡状態になります.この推移は非平衡状態にあり,時間的経過に伴う現象の推移が問題になります.ところが生物系などの開放系は,常に外界とのエネルギーのやりとりをしており,熱平衡状態にならないし,又,本質的に非線形現象です.こうした系の時間的変動を時系列データとして観測し,これをスペクトル解析する場合に,設問のようなことが問題になります.ところがスペクトル解析というのは,数学的変換(フーリエ変換)にすぎないものですから,現象の特性がどうであれ(非線形であれ,非平衡であれ),そうした現象の特性に無関係に解析されることができなければなりません.非線形現象や非平衡現象,あるいはゆらぎの性質に特有の解析法があるわけでなく,全く普遍的な解析法を用いて,逆にこれらの現象の特性を引き出すことができなければならないのです. |
|
|
問 “ボゴリューボフマップ”というものを見ましたが,何のことか解りません.これは一体何を意味しているのですか? |
0220 |
|
答 何らかの初期的変動(初期混沌過程)から次第に系全体が平衡化し,最終的には熱平衡状態になる時間的経過に伴う現象の推移について,ボゴリューボフ(Bogoljubov)は図0220のように示しました.物理現象を定式化する場合,平衡・非平衡,線形・非線形,定常・非定常といった現象の区分が必要であり,それが時間の経過とどう関連しているかを理解する上で,このマップは大切なものです.
|
|
|
問 時系列データの解析に統計学を適用することはできるのでしょうか? |
0230 |
|
答 例えば相互に独立なデータを扱う場合,その有用性は別にして,統計学という理論体系が確立しています.ところが,時系列データについて観測値の間に統計的独立性が仮定できず,したがって統計学をその解析に適用することは本質的にできません.そして,そのような時系列データを扱う総合的・汎用的・整合的な理論体系が未だ構築されていません.しかし現実には,統計学を用いて解析する報告が後を断ちません.時系列データに統計学を適用する場合,あくまでも一つの目安としての意味しか持ち得ません.このことを無視して(理解しないで)適用することにこそ,「混乱」の第一の原因があると考えられます. |
|
|
問 時系列データのあてはめ曲線のはどのようにして求められるのでしょうか? |
0240 |
|
答 時系列データのあてはめ曲線には,さまざまな函数系が考えられますが,最も一般的なのは,時系列の周期函数をフーリエ級数展開,
で表すものです.与えられた時系列データに最も良くあてはまる周期函数を得るために,水準値{a0},振幅値{an,bn},周期値{Tn}が決定されます.一般にこの手続きは,非線形最小2乗法になります.しかしこの手続きは,基本周期T0の整数倍の周期しか対象にならず,全く任意の時系列には適用できません.MemCalcはこの問題も克服しています.詳しくは問0950を参照してください. |
|
|
問 時系列データのあてはめ曲線が妥当であることを示す,統計における検定のような指標はありますか? |
0250 |
|
答 非線形最小2乗法では,一般に,時系列データのうちあてはめ曲線によっては記述できない部分を0のまわりに正規分布する誤差とみなし,その2乗和が最小になるところであてはめ曲線のパラメータを決定します.しかしながらここでは,誤差の2乗和を局所的に最小にする,初期値に依存する解が得られるだけであり,それが唯一の最適な解である保証はありません.また,あてはめ曲線では説明できない部分を“誤差”と見なせる保証はどこにもありません. |
|
|
問 時系列データにあてはめた曲線の妥当性は,どのようにして評価できるのでしょうか? |
0260 |
|
答 この評価は,非線形最小2乗法を用いる限り,これまでは全く不可能でした.しかしMemCalcを用いることにより,この妥当性の評価も可能になりました.MemCalcによって決められたあてはめ曲線を構成するのに用いた周期値が極めて正確であること,およびあてはめ曲線を周期関数の和として表現できることを実証したことによります.詳しくは,問0960で説明します. |
|
|
問 例えば,主成分分析とか,そのような方法はあてはめ曲線の妥当性の指標として使えませんか?また,それはなぜですか? |
0270 |
|
答 多変量解析であてはめ曲線を求めることは形式上できます.形式上といったのは,多変量解析では,独立変数と従属変数をどうとるかが決定的なことになるのです.時系列では何を独立変数に決めることができるか,という未解決の問題があるため,多変量解析であてはめ曲線を求めることは本質的に困難であると言えます. |
|
|
問 パターン認識などの手法はあてはめ曲線の妥当性の指標として使えませんか? |
0280 |
|
答 パターン認識の手法の基本は,マッチングにあり,あらかじめ教師信号のような形であてはめ曲線を備えていることが必要となりますが,時系列ではあらかじめ備えることが不可能であり,時系列のあてはめ曲線を求めることはできないものと考えられます.しかし,限られた変動パターンの識別は可能であると考えられます. |
|
|
問 いわゆるペリオドグラムの方法によれば,それが妥当な周期であるか否かが判定できると聞きました.これは本当に可能なのでしょうか? |
0290 |
|
答 ペリオドグラム(periodgram)とは,スペクトル(PSD)を真のPSDの推定量によって置き換えるものであり,最大の問題点は自己相関関数の推定量を計算することを前提にしなければならないことにあり,さらに理論的には,PSDを求めるフーリエ変換の離散的近似であって,本質的にFFTや一般調和解析などがかかえる問題を克服できません.時系列変動に含まれる周期は,含まれる数の莫大さに加えて,必ずしも離散的周期とはならず,ある周期値を中心にして連続的分布をもつ場合があります.こうした時系列周期をペリオドグラムで扱うことは本質的に不可能です. |
|
|
問 例えば“Articial Life”という分野では,モデルを構築してそれをコンピュータで解くことによって,ヒトがこれまで観測したことのない現象(生命進化,生命の誕生など)を理解しようと試みていますが,このような場合でも,「観測データの絶対的とも言える優位性がある」と言えるのでしょうか? |
0300 |
|
答 物理的実在が示すデータとモデルが発生するデータとは本質的に違うものであることを十分に踏まえることが大切です.観測したことのない現象について,モデルが示すデータは必ずこの実在性について現象が示すデータによって検証されることが必要で,これが出来ない場合は,あくまでもそのモデルという限定つきでの優位性にすぎないものです. |
|
|
問 時系列データを与えて,それがどれほど規則的であるか,または乱雑であるかを定量的に評価することはできますか?例えば24時間を基本モードとする日内リズムだけをもつ時系列と,加えて一週間を基本モードとするリズムをもつ2つの時系列データではどうなりますか? |
0310 |
|
答 時系列変動は,基底変動+ゆらぎという形式をとり,基底変動は一見いくら乱雑に見えてもこれは規則的変動(決定論的変動)になります.従って,ゆらぎの部分について規則的か乱雑であるかの評価をすることになりますが,もともと,基底変動の決定自体が自明なことでなく,時系列の乱雑さの程度の定量的決定は容易なことではありません.その上で,一般的には,エントロピー概念が適用可能になります. |