|
���Q�@�X�y�N�g����͈��
|
|||
|
��@MemCalc�ł́C�ǂ̃X�y�N�g����͖@��p���Ă���̂ł����H�܂������I���R�͉��ł����H |
0560 |
||
|
���@MemCalc�ł́C�ő�G���g���s�[�@(MEM)��p���Ă��܂��DMemCalc��MEM��p���Ă��闝�R�̈�́C�\0550�ɂ���悤�ɁCMEM�͒Z���f�[�^�̉��(�^����ꂽ�f�[�^�ȊO�̃f�[�^��K�v�Ƃ��Ȃ�)�C�����ĕ���\�ɗD��Ă��邩��ł��DMEM�́C�o�|�O(Burg)�ɂ���ăX�y�N�g����͖@�Ƃ��Ċm������܂����D�������Ȃ���C�o�|�O�ɂ���Ă����炳�ꂽ�A���S���Y���𒉎��ɃR���s���|�^�E�v���O�����Ƃ��Ď������邱�Ƃ́CMemCalc�ȑO�ɂ͏\���������Ă����Ƃ͎v���܂���DMemCalc�ł͏]����MEM�ɂ����������������Ă���CMEM�̗D�ꂽ���������߂Ĕ������ꂽ�ƌ����Ă����ł��傤�D |
|||
|
��@MemCalc�ł͂ǂ̂悤�ɏ]����MEM�̍�����������Ă���̂ł����H |
0570 |
||
|
���@�]����MEM�ł̓X�y�N�g�������₻����ߒ���AR�@�ɂ��莮���Əd�Ȃ镔�������݂��Ă���CMEM�̖{�i�I���p��AR�@�̌��E�ɂ���đ傫�����Ȃ��Ă��܂����D���̍ł��傫�ȓ_�́CAR�@�ɂ�郉�O�l(�����̏ꍇ�C���ɏ����Ȓl�ɂȂ�)��p���Ȃ���Ȃ�Ȃ��Ƃ����Ԉ�����������܂���ʂ������߂ł��DMemCalc�ł́CMEM�͖{��AR�@�̌��E�ɂ���čS��������̂ł͂Ȃ��Ƃ����V�����������̗p���C���O�l���\�Ȍ���傫������Ƃ�����_�ȕ��@���̗p���܂����D���͂��̂��Ƃɂ���āC�]����MEM�̌��E�������ɍ����ł����̂ł��D |
|||
|
��@MEM�Ƃ͂ǂ��������̂ł����H |
0580 |
||
|
���@MEM�́C���v�����w�̊�b���_�Ƃ��ăW�F�C���Y(Jaynes)�ɂ���Ē�N���ꂽ�g�ő�G���g���s�|����(ME���� maximum entropy
principle)�h�Ɋ�Â��X�y�N�g������@�ł��D�����CMEM�̈˂��ė����_�I��b�́C���v�����w�ɂ������b���_�Ƃ��Ă�ME�����ɂ���܂��DME�����́C���G���g���s�|�̕��ՓI�����Ɋ�Â����Ռ����ł����āC�����ł͂Ȃ��ƌ����Ă��܂��D�����Ă���ME�����́C���v�����w���C���̍ł���{�I�ȉ����ł���g�挱�I���m���̌����h���������܂����D |
|||
|
��@AR�@�Ƃ͂ǂ��������̂ł����C�܂��gAR�@�̌��E�h�Ƃ͂ǂ̂悤�Ȃ��̂ł����H |
0590 |
||
|
���@AR�@�̌��E�ɂ́C�傫�������Ď��̂Q������܂��D
�ȉ��ł́C�@�ƇA�ɂ��āC���ɐ������܂��D |
|||
|
��@AR�@�̃��f���̌��E��������͂���܂����H |
0600 |
||
|
���@Barnes ��́CARMA(���ȉ�A�ړ����� autoregressive moving average)���f��(AR���f����MA(�ړ�����
moving
average)���f����g�ݍ��킹�����f��)�Ɋ�Â��āC���z���_���̕ϓ���6000�N�ɂ킽��V�~�����|�V��������Ă��܂��DARMA���f���́CAR���f���ɉߋ��̌덷(���O�t���덷)���܂߂�Ƃ������f���ł��D�ߋ��̌덷�͊ϑ�����Ȃ��̂Ŕ��F�G���Ƃ��Ĉ����܂��D��������MA���f����AR���f���Ƃ̌����ɂ���āC�����̎��n��f�|�^�̉�͂�AR���f���Ɣ�ׂĂǂ̂悤�ȑO�i�������炵�Ă��邩�͂���قǖ��炩�ɂ͂Ȃ��Ă��܂���DAR���f���ɂ́C���̑���ARIMA(���ȉ�A�a���ړ����� autoregressive
integrated-moving)���f���ƌ������X�ɋZ�I�I�ȃ��f��������܂����C�ǂ̎��n��ɂǂ̃��f�����K�ł��邩�肷�邱�Ƃ͔��ɓ�����ł��D�����Č����CAR���f���̑Ó����͌����̎��n����ǂ̒��x�����ł��邩�ɂ������Ă��܂����C���̓_�ł͈�т��ėl�X�ȋ^�₪�����Ă��܂��D���n���͕��@�������̎��n����ǂ̒��x�����ł��邩�Ƃ����_�́C���_�I�W�J�⋻���ȏ�́C���n���͕��@�̐^���肷��ł��d�v�Ȋ�ł��D
�@
|
|||
|
��@�悭MEM��AR(���ȉ�A���f��)�͓����ł���Ƃ����܂����C���̓_�ɂ��͂ǂ��ł����H |
0610 |
||
|
���@AR�������ς�Ƃ��錤���҂�AR�̔��e��MEM�𗝉����悤�Ƃ���X���������悤�ł��D�������Ȃ���CMEM��AR�͕ʂ̂��̂ł���Ƃ���̂����������߂ł��D����C�����̌����҂�MEM���L�����p�����ɏ]���āC���̂悤�ȗ������}���ɐi�ނƍl�����܂��D |
|||
|
��@�����̉�����ł�AR�̗��_�̌n�̂Ȃ���MEM�X�y�N�g���������Ă��܂��DAR�̗��_�̌n�𗣂��MEM�X�y�N�g���o����܂ł̑̌n���\�z�ł���̂ł��傤���H |
0620 |
||
|
���@���Ƃ���MEM�Ɋւ���Burg�ɂ��ŏ��̌����ł�,AR���f���Ƃ͂܂��������W�ɗ��_���\������Ă��܂����D�܂��CMEM�Ɋւ��錤���̓����̏W�听�ł���D.G.Childers��"Modern
Spectrum Analysis"(1978)�Ɍf�ڂ���Ă��鐔�X�̘_���ł́CMEM�X�y�N�g���̈�����AR���̂���Ƃ܂������قȂ�C���ʂƂ���MEM��AR�͕ʕ��ł���ƒ��҂炪�l���Ă��邱�Ƃ��悭�ǂݎ��܂����CAR�ɂ܂������W����MEM�X�y�N�g���o����܂ł̗��_�̗��ꂪ�L����Ă��܂��D |
|||
|
��@MEM��AR�ł̓X�y�N�g���̌v�Z�̍ۂɓ��������g���܂��D���̓_���炷��ƁC��͂藼�҂͓����Ȃ̂ł͂Ȃ��ł����H |
0630 |
||
|
���@MEM�̗��_�̌n�C��̓I�ɂ��̃X�y�N�g���v�Z�̂��߂̎葱���͌����ɑ��݂��邷�ׂĂ̎��n��f�[�^�ɂ���(�G���S�[�h���̉���͒ʏ�ǂ��萬������Ƃ���)�K�p�\�ł��D����CAR�͐��`���f���ɂ��Ă̂ݐ������闝�_�ł��D���ėp��MEM�̗��_�̌n�������肳�ꂽAR�̏ɂ����Ă��������邱�Ƃ́CMEM�̗��_�̌n�̕�����ʂɐ������邱�Ƃ��������̂ł��D |
|||
|
��@AR�ł͊e����ʋK��(FPE�CAIC�CCAT)��p���ăX�y�N�g���v�Z�̍ۂ̃��O�����肵�C�]���ė^����ꂽ���n��f�[�^�ɂ��ėB��̃X�y�N�g���邱�Ƃ��ł��܂��DMEM�ł͂ǂ��Ȃ�܂����H |
0640 |
||
|
���@�B��̃X�y�N�g�������߂邽�߂ɂ́C�A���I�ɑ��肳�ꂽ�������̃f�[�^���K�v�ł��D���̂��Ƃ͑����C(���U�I�ɑ��肳�ꂽ)�L�����̃f�[�^�C�^����ꂽ�����̎��n��f�[�^�݂̂�p���ėB��̃X�y�N�g�������߂邱�Ƃ͖{���s�\�ł��邱�Ƃ��Ӗ����܂��D |
|||
|
��@AR�ł̓��O�̒l�͂ǂ̂悤�ȈӖ��������܂����H |
0650 |
||
|
���@AR�̏ꍇ�C���O�̒l�͎��n��f�[�^�������V�X�e���̍\�����̂��̂ɒ������Ă��܂��D�Ⴆ���O�̒l���Q(=�Q����AR�ߒ�)�ł���Ƃ́C�ϑ��l���P�O�ƂQ�O�̊ϑ��l�ɂ���Ă̂��܂�C���̂悤�ȍ\���������̂Ƃ��đΏیn�𗝉�����Ƃ������Ƃł��D����CMEM�̃��O�l�́C�X�y�N�g���̕���\�Ƃ̊W�Ŏ��n������錩��(��)�ł��D |
|||
|
��@�����AR���f���ƌ����Ă����낢��Ƃ���̂ł͂���܂��H |
0660 |
||
|
���@ARMA�CARIMA�ȂǁC�g����I�ȃ��f���h�Ƃ�����Q�̃��f��������܂��D�������Ȃ���C����������`���f���Ƃ����_�ł͑卷�����C�������ǂ̎��n��f�[�^�ɑ��Ăǂ̃��f����K�p���ׂ����Ƃ�����ӓI�Ȋ������܂���D����C�g�J�I�X�h�Ɋւ���ŋ߂̌����̎����Ƃ���ɂ��C���̃f�[�^�C�o�σf�[�^���͂��߁C�������������ɏo��قƂ�ǂ̃f�[�^�͔���`�V�X�e������̏o�͂ł��D�J�I�X���n��f�[�^��AR���f���ʼn�͂����Ȃ����Ƃ͖��炩�ł��D |
|||
|
��@���O�̐ݒ�Ɋւ��āCAR���̃��O�̒l�ƈقȂ�ݒ���N�C�܂��͎��s���Ă�����m�肽���̂ł����D |
0670 |
||
|
���@�����F���ƃu���s�A�j(Rovelli&Vulpiani,
1983)�́C��X�̒n�������w���n��f�[�^�ɑ��āC�������̃��O�l
M ��p���邱�Ƃɂ���ē�����PSD�̐U�镑������܂����D�}0670�ɁC�ނ�ɂ���ĕ��ꂽPSD���C�f�[�^�̑S��N
��10, 20,..., 80���ɓ��������O�ɑΉ������Ď����܂��D�ނ�́C�ʏ�̋K��(FPE, AIC�����CAT)�ɂ���ė^������M�̒l(N�̐����ɓ�����)����C�X�ɐV�����K���Ƃ���CCT�����CCCT�ɂ��M�̒l��N�̐�10���ɂȂ邱�Ƃ���܂����D�ނ�́C�Ⴆ�Α��z���_���ɂ��ẮC204�W�{�_�ɂ��āCFPE,
AIC�����CAT�K������C���ꂼ��CM
= �W, �R����тX����C�p�h�}�i�r�����ƃ��I(Padmanabhan
& Rao)�́C�܂��C316�W�{�_�̃f�[�^�ɂ���M =
�X����܂����D
|
|||
|
��@�AR�ł͗^����ꂽ���n��f�[�^�̃X�y�N�g�������߂�̂ł͂Ȃ��C���̎��n��f�[�^�̑������W�c�̃X�y�N�g�������߂Ă���̂ł��邩��C���O���������Ă悢�D�t�Ƀ��O��傫������Ƃ��̎��n��f�[�^�ɂ̂ŗL�̃X�y�N�g�������߂邱�ƂɂȂ�C������ߏ肠�Ă͂߂̏�ԂƂȂ�s�K���D��Ƃ̎w�E���܂����D |
0680 |
||
|
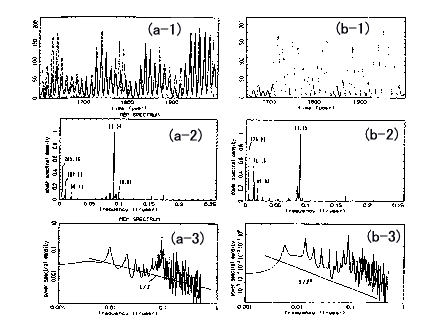
���@�X�y�N�g���s�[�N���猴���n��f�[�^���\�����郂�[�h����肾���C���̕������[�h�ɂ���͔����Ƃ��Č����n��f�[�^�̋������������Ƃ���MemCalc�V�X�e���ł́C���O��傫���Ƃ��Ď��n��f�[�^�ɌŗL�̃��Y�����X�y�N�g���̃s�[�N�Ƃ��Ď��o�����Ƃ��K�v�ł��D���̈�A�̎葱����AR���ɉ��߂���Ƣ�ߏ肠�Ă͂߂ňӖ����Ȃ���Ƃ������ƂɂȂ�悤�ł��D
|