|
§2 スペクトル解析一般
|
|
|
問 MemCalcで,スペクトル解析法として一般的に良く用いられているFFTよりもMEMを用いる理由はなんですか? |
0690 |
|
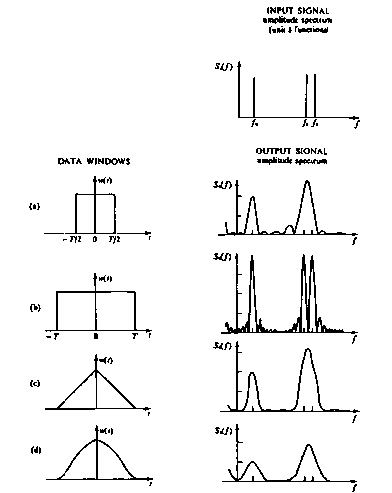
答 FFTは,時系列のモデルであるAR法とは違って,単なる数学的変換(フ−リエ変換 Fourier transformatiom)手続きに過ぎないので,理論構成上の問題点はありません.しかし問題は,−∞から+∞までの時系列に対する理論になっていることから生じます.即ち,“現実のデ−タの有限性”(問0060参照)との不整合が生じます.このため,有限時系列デ−タを−∞から+∞まで周期的に延長し,延長部分の影響を打ち消すために各種のウインドウ関数(window function)によるフィルタ−を導入しなければならないなどの,人為的操作が不可避となります.このために,図0690のFFT-PSDに見られるように,偽のスペクトル・ピ−クの出現の問題やスペクトル分解能が低下する問題が生じます.一方,MEMではデータに人為的操作を施す必要がないので,MEM-PSDに観測されるスペクトル・ピークは,データの周期構造のみを反映します.
|
|
|
問 “偽りのスペクトル・ピーク”であるか否かはどのように検証しているのですか?またその検証は可能なのですか? |
0700 |
|
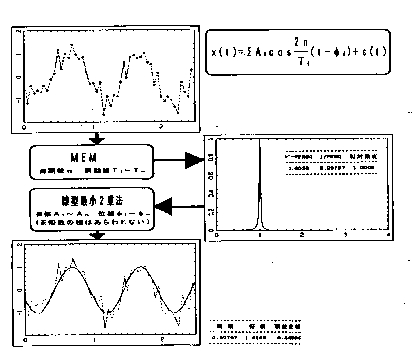
答 これまでのスペクトル解析の一つの問題点は,得られたスペクトルの妥当性を検証する方法が確立していないことです. そこで私たちは,周波数領域の解析(スペクトル解析)としてのMEMを,時間領域の解析(時系列の再現)としての非線形最小二乗あてはめ法に組み合わせることによって,このスペクトルの妥当性を検証する方法をMemCalcに確立することに成功しました.即ち,得られたスペクトルから求められる周期値が,元の時系列を再現するのかどうかを,MemCalcの最小二乗あてはめル−チンを使って確かめます.図0700に,周波数領域の解析と時間領域の解析の流れを示します.同図では,MEMによって得られた周期構造を用いて,非線形最小2乗法が線形化されることによって,解の一義性が保証されているのがわかります.
|
|
|
問 MEM-PSDのほうがFFT-PSDよりも妥当であることを示す例はありますか? |
0710 |
|
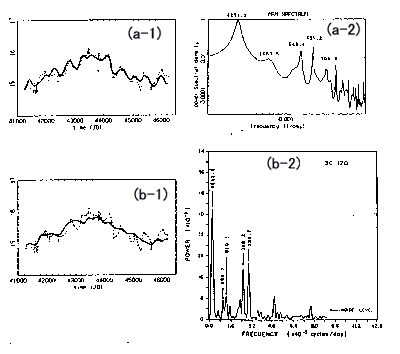
答 図0710に,MEM-PSDとFFT-PSDによって観測されたスペクトル・ピークの妥当性を検証した例を示します.
図0710(a-1)および(b-1)の点線は,銀河3C-120の光度の変動時系列デ−タです.Webb らはこのデ−タをFFTで解析しPSDを得ています(図0710(b-2)).そこで,図0710(b-2)に記載されている5つの主要な周期値を使って元の時系列の再現を試みたところ,山なりのおおきな周期の振動(周期値4543.9による)は再現されるますが,それより小さな周期の振動は十分再現されいないという結果を得ました.これはFFTで求めた周期値が,特に999.7以下の周期値が,その妥当性を欠いていることを意味しています.
|
|
|
問 FFTでもウィンドウの問題を別にすれば“唯一のスペクトル”を求めることができるのではないですか? |
0720 |
|
答 確かに与えられた時系列データを用いて“唯一のスペクトル”が求まります.しかしFFTでは与えられた時系列データが無限の過去から無限の未来まで周期的に繰り返される,そのような無限長データのスペクトルを求めていることに注意が必要です.即ちFFTは与えられた時系列データのスペクトルを求めるかわりに,そのデータが無限に繰り返される無限長データのスペクトルを出してくるのです.これはFFTの理論構成上の必然で,FFTを用いる限り,この制約から逃れる術はありません.無限長のデータですから,唯一のスペクトルを求めることができるのです.このとき,ウィンドウはおなじパターンの繰返しのもたらす困難(ゴーストピークの出現など)を低減するために用いられます.他方,MEM(Burg法)では,与えられた時系列データ以外,一切の構造を仮定しません. |
|
|
問 データ長を長くとればFFTでも低周波数領域でそこそこの結果が得られるのではありませんか? |
0730 |
|
答 確かにデータ長を長くとり,また(計算点を周密にとれないFFTの短所を回避するために)サンプリング間隔を短くとることによって改善されます.しかし,そのように準備された長いデータがもとの短いデータと“同種の”データであるかが,時として問題になります.先述した多重周期構造をもつ時系列(問0090参照)の場合,データ長をどう選択するかは極めて重大な意味をもちます.更に,例えば一定時間ごとに血圧を測定するABPMシステムの場合,短い間隔で長期間にわたり測定を繰り返すことは,被験者によっては相当な負担となり,結果は日常生活での通常の血圧変動とまったく異なるものとなることも危惧されます. |
|
|
問 FFTが多くの困難を抱えるにもかかわらず,実際にはFFTの方がMEMよりも多く用いられているのは何故でしょうか? |
0740 |
|
答 一口で言えば,スペクトル解析法の発展段階の問題です.つまり,たまたまFFTの方が理論的に分かり易く,且つコンピュータ・プログラム化し易かったことによります.これに対してMEMは,その考え方,理論,そしてプログラム化において容易に理解できるものではありませんでした.この点については問0780を参照してください. |